achilleas έγραψε: ↑Παρ Ιουν 03, 2022 9:13 pm
Έστω οξυγώνιο σκαληνό τρίγωνο

,

το σημείο τομής της διχοτόμου της γωνίας

με την πλευρά

και

το ίχνος του ύψους από το

. Έστω ότι η μεσοκάθετος του ευθύγραμμου τμήματος

τέμνει τα ημικύκλια διαμέτρου

και

που κατασκευάζονται στο εξωτερικό του τριγώνου

στα σημεία

και

, αντίστοιχα. Να αποδειχθεί ότι τα σημεία

,

,

και

είναι ομοκυκλικά.
Ας δούμε λίγο πιο γενικά το πρόβλημα (δεν είναι ανάγκη το

να είναι ύψος του τριγώνου.
Δίνεται οξυγώνιο και σκαλινό τρίγωνο  και ας είναι
και ας είναι  τα σημεία τομής των περίκυκλων
τα σημεία τομής των περίκυκλων  των τριγώνων
των τριγώνων  με τη μεσοκάθετη της διχοτόμου
με τη μεσοκάθετη της διχοτόμου  του
του  που βρίσκονται εξωτερικά αυτού, με
που βρίσκονται εξωτερικά αυτού, με  τυχόν σημείο της πλευράς του
τυχόν σημείο της πλευράς του  . Να δειχτεί ότι
. Να δειχτεί ότι  είναι ομοκυκλικά.
Απόδειξη
είναι ομοκυκλικά.
Απόδειξη

- ομοκυκλικά.png (94.18 KiB) Προβλήθηκε 865 φορές

Έστω

τα μέσα των

αντίστοιχα . Τότε προφανώς

συνευθειακά και ας είναι

το σημείο τομής της διακέντρου

των κύκλων

με την κοινή τους χορδή

. Προφανώς

το μέσο της

(η διάκεντρος τεμνομένων κύκλων είναι μεσοκάθετη στην κοινή τους χορδή) , οπότε

συνευθειακά και έστω

.

Με

προκύπτει ότι οι τετράδες

είναι ομοκυκλικές σε κύκλους διαμέτρων

αντίστοιχα.
Έχουμε:

και ομοίως

.

- ομοκυκλικά.png (94.18 KiB) Προβλήθηκε 865 φορές

Επίσης

και

. Από
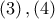
προκύπτει ότι τα ισοσκελή τρίγωνα (λόγω ακτινών και μεσοκαθέτου)

είναι όμοια (από μια γωνία των «βάσεών» τους ίση) και συνεπώς

ομοκυκλικά , όπου

όπως επίσης και (εξ’ αιτίας της διχοτόμου

διχοτόμος της γωνίας

του τριγώνου


Έτσι έχουμε:





ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
 ,
,  το σημείο τομής της διχοτόμου της γωνίας
το σημείο τομής της διχοτόμου της γωνίας  με την πλευρά
με την πλευρά  και
και  το ίχνος του ύψους από το
το ίχνος του ύψους από το  . Έστω ότι η μεσοκάθετος του ευθύγραμμου τμήματος
. Έστω ότι η μεσοκάθετος του ευθύγραμμου τμήματος  τέμνει τα ημικύκλια διαμέτρου
τέμνει τα ημικύκλια διαμέτρου  και
και  που κατασκευάζονται στο εξωτερικό του τριγώνου
που κατασκευάζονται στο εξωτερικό του τριγώνου  στα σημεία
στα σημεία  και
και  , αντίστοιχα. Να αποδειχθεί ότι τα σημεία
, αντίστοιχα. Να αποδειχθεί ότι τα σημεία  ,
,  ,
,  και
και  είναι ομοκυκλικά.
είναι ομοκυκλικά.
 και ας είναι
και ας είναι  τα σημεία τομής των περίκυκλων
τα σημεία τομής των περίκυκλων  των τριγώνων
των τριγώνων  με τη μεσοκάθετη της διχοτόμου
με τη μεσοκάθετη της διχοτόμου  του
του  είναι ομοκυκλικά.
είναι ομοκυκλικά. Έστω
Έστω  τα μέσα των
τα μέσα των  αντίστοιχα . Τότε προφανώς
αντίστοιχα . Τότε προφανώς  συνευθειακά και ας είναι
συνευθειακά και ας είναι  το σημείο τομής της διακέντρου
το σημείο τομής της διακέντρου  των κύκλων
των κύκλων  συνευθειακά και έστω
συνευθειακά και έστω  .
. προκύπτει ότι οι τετράδες
προκύπτει ότι οι τετράδες  είναι ομοκυκλικές σε κύκλους διαμέτρων
είναι ομοκυκλικές σε κύκλους διαμέτρων  αντίστοιχα.
αντίστοιχα.  και ομοίως
και ομοίως  .
.
 και
και  . Από
. Από 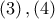 προκύπτει ότι τα ισοσκελή τρίγωνα (λόγω ακτινών και μεσοκαθέτου)
προκύπτει ότι τα ισοσκελή τρίγωνα (λόγω ακτινών και μεσοκαθέτου)  είναι όμοια (από μια γωνία των «βάσεών» τους ίση) και συνεπώς
είναι όμοια (από μια γωνία των «βάσεών» τους ίση) και συνεπώς  ομοκυκλικά , όπου
ομοκυκλικά , όπου  όπως επίσης και (εξ’ αιτίας της διχοτόμου
όπως επίσης και (εξ’ αιτίας της διχοτόμου  διχοτόμος της γωνίας
διχοτόμος της γωνίας  του τριγώνου
του τριγώνου 




 ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
ομοκυκλικά και το ζητούμενο έχει αποδειχθεί. και έχουμε:
και έχουμε: 

 θα έχουμε
θα έχουμε 
 γράφεται ως
γράφεται ως ![\displaystyle 2\sin u \left [\cos u\cos \left ( B-\frac{A}{2}+y \right )-\sin u\sin \left ( B-\frac{A}{2}+y \right ) \right]= \displaystyle 2\sin u \left [\cos u\cos \left ( B-\frac{A}{2}+y \right )-\sin u\sin \left ( B-\frac{A}{2}+y \right ) \right]=](/forum/ext/geomar/texintegr/latexrender/pictures/74ae2bae61096ca6b3419445740f26fb.png)





 θα έχουμε:
θα έχουμε:
 γράφεται ως
γράφεται ως ![\displaystyle 2\sin z\left [ \cos \left ( \frac{A}{2}+B+y \right )\cos z+\sin \left ( \frac{A}{2}+B+y \right )\sin z \right ]= \displaystyle 2\sin z\left [ \cos \left ( \frac{A}{2}+B+y \right )\cos z+\sin \left ( \frac{A}{2}+B+y \right )\sin z \right ]=](/forum/ext/geomar/texintegr/latexrender/pictures/4b95a3729f7989db550db02d988c6357.png)



 προκύπτει ότι
προκύπτει ότι  κι επιδή οι γωνίες είναι κυρτές και άνισες προκύπτει ότι είναι παραπληρωματικές οπότε
κι επιδή οι γωνίες είναι κυρτές και άνισες προκύπτει ότι είναι παραπληρωματικές οπότε 
 προκύπτει ότι
προκύπτει ότι  όπως θέλαμε.
όπως θέλαμε.