achilleas έγραψε: ↑Τετ Ιουν 15, 2022 6:19 pm
Έστω τρίγωνο

και έστω

το έγκεντρο του. Έστω

το σημείο τομής της

με την

. Έστω

το έγκεντρο του τριγώνου

και έστω

, το έγκεντρο του

. Έστω ότι η ευθεία

τέμνει τον περιγεγραμμένο κύκλο του τριγώνου

στο σημείο
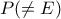
και έστω ότι η ευθεία

τέμνει τον περιγεγραμμένο κύκλο του τριγώνου

στο σημείο
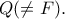
Να δειχθεί ότι το μέσο της

ανήκει στον περιγεγραμμένο κύκλο του τριγώνου
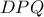
.
Φιλικά,
Αχιλλέας
Έστω

το μέσον της

.
Ισχυρισμός 1: 
και

.
Απόδειξη: Έστω
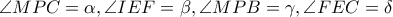
. Τότε παρατηρούμε πως
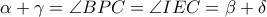
Από το Λήμμα (δείτε στο τέλος της απόδειξης), αρκεί να δείξουμε πως
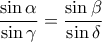
.
Είναι,
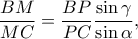
οπότε αφού

, είναι
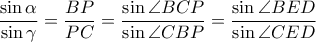
Αφού όμως
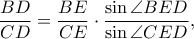
είναι τελικά
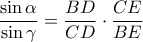
Επιπλέον,
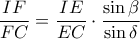
,
και άρα
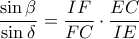
Συνεπώς αρκεί να αποδείξουμε πως
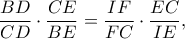
ή ισοδύναμα ότι
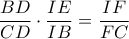
Αυτή όμως ισχύει διότι, από το Θεώρημα Διχοτόμων,
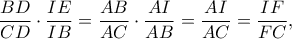
όπως θέλαμε
 Ισχυρισμός 2:
Ισχυρισμός 2: Το τετράπλευρο

είναι εγγράψιμο.
Απόδειξη: Είναι λόγω της εγγραψιμότητας των
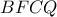
και
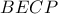
,
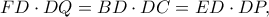
οπότε το

είναι εγγράψιμο

Στο πρόβλημα, από τους Ισχυρισμούς 1 και 2 είναι
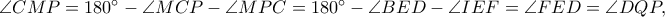
οπότε το τετράπλευρο
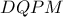
είναι εγγράψιμο, και η απόδειξη ολοκληρώθηκε.
Λήμμα: Αν

γωνίες ώστε
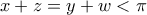
και
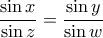
, τότε

και
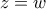
.
Απόδειξη: Έστω η συνάρτηση
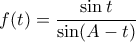
, όπου
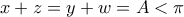
, οπότε
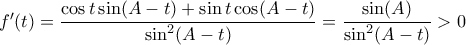
καθώς

.
Άρα η

είναι γνησίως αύξουσα, οπότε και 1-1, συνεπώς αφού
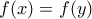
έπεται ότι

και συνεπακόλουθα και
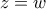

 και έστω
και έστω  το έγκεντρο του. Έστω
το έγκεντρο του. Έστω  το σημείο τομής της
το σημείο τομής της  με την
με την  . Έστω
. Έστω  το έγκεντρο του τριγώνου
το έγκεντρο του τριγώνου  και έστω
και έστω  , το έγκεντρο του
, το έγκεντρο του  . Έστω ότι η ευθεία
. Έστω ότι η ευθεία  τέμνει τον περιγεγραμμένο κύκλο του τριγώνου
τέμνει τον περιγεγραμμένο κύκλο του τριγώνου  στο σημείο
στο σημείο 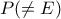 και έστω ότι η ευθεία
και έστω ότι η ευθεία  τέμνει τον περιγεγραμμένο κύκλο του τριγώνου
τέμνει τον περιγεγραμμένο κύκλο του τριγώνου  στο σημείο
στο σημείο 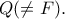 Να δειχθεί ότι το μέσο της
Να δειχθεί ότι το μέσο της  ανήκει στον περιγεγραμμένο κύκλο του τριγώνου
ανήκει στον περιγεγραμμένο κύκλο του τριγώνου 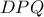 .
. 
 το μέσον της
το μέσον της  και
και  .
.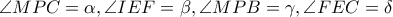 . Τότε παρατηρούμε πως
. Τότε παρατηρούμε πως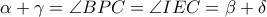
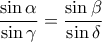 .
.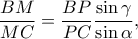
 , είναι
, είναι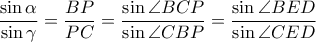
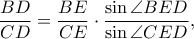
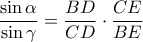
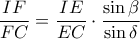 ,
,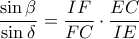
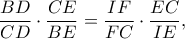
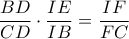
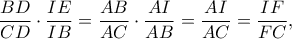

 είναι εγγράψιμο.
είναι εγγράψιμο.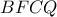 και
και 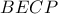 ,
,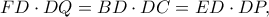
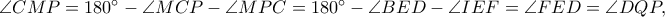
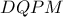 είναι εγγράψιμο, και η απόδειξη ολοκληρώθηκε.
είναι εγγράψιμο, και η απόδειξη ολοκληρώθηκε. γωνίες ώστε
γωνίες ώστε 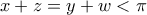 και
και 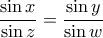 , τότε
, τότε  και
και 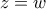 .
.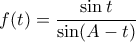 , όπου
, όπου 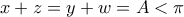 , οπότε
, οπότε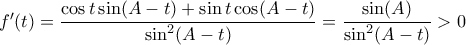
 .
. είναι γνησίως αύξουσα, οπότε και 1-1, συνεπώς αφού
είναι γνησίως αύξουσα, οπότε και 1-1, συνεπώς αφού 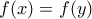 έπεται ότι
έπεται ότι