 με
με  Στην προέκταση της πλευράς
Στην προέκταση της πλευράς 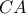 θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο ώστε
τέτοιο ώστε  Η μεσοκάθετος του τμήματος
Η μεσοκάθετος του τμήματος  τέμνει την εσωτερική και την εξωτερική διχοτόμο της γωνίας
τέμνει την εσωτερική και την εξωτερική διχοτόμο της γωνίας  στα σημεία
στα σημεία  και
και  , αντίστοιχα. Να δείξετε ότι τα σημεία
, αντίστοιχα. Να δείξετε ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, rek2
 με
με  Στην προέκταση της πλευράς
Στην προέκταση της πλευράς 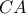 θεωρούμε σημείο
θεωρούμε σημείο  τέτοιο ώστε
τέτοιο ώστε  Η μεσοκάθετος του τμήματος
Η μεσοκάθετος του τμήματος  τέμνει την εσωτερική και την εξωτερική διχοτόμο της γωνίας
τέμνει την εσωτερική και την εξωτερική διχοτόμο της γωνίας  στα σημεία
στα σημεία  και
και  , αντίστοιχα. Να δείξετε ότι τα σημεία
, αντίστοιχα. Να δείξετε ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.Έστω
 η εσωτερική διχοτόμος του ισοσκελούς τριγώνου
η εσωτερική διχοτόμος του ισοσκελούς τριγώνου  , οπότε θα είναι και ύψος και διάμεσος , άρα
, οπότε θα είναι και ύψος και διάμεσος , άρα  το μέσο της
το μέσο της  και
και  . Αν
. Αν  τότε με
τότε με  μεσοκάθετη της
μεσοκάθετη της  θα είναι
θα είναι  το μέσο της
το μέσο της  ,
,  και το τετράπλευρο
και το τετράπλευρο  θα είναι «χαρταετός», άρα
θα είναι «χαρταετός», άρα  και φυσικά (από την εξωτερική διχοτόμο
και φυσικά (από την εξωτερική διχοτόμο 
 εγγράψιμο σε κύκλο , οπότε
εγγράψιμο σε κύκλο , οπότε 
 το τμήμα
το τμήμα  συνδέει τα μέσα των πλευρών του
συνδέει τα μέσα των πλευρών του  άρα
άρα  είναι ομοκυκλικά , άρα
είναι ομοκυκλικά , άρα  .
. και
και  με τρία κοινά σημεία
με τρία κοινά σημεία  προκύπτει ότι
προκύπτει ότι  είναι ομοκυκλικά και το ζητούμενο έχει αποδειχθεί.
είναι ομοκυκλικά και το ζητούμενο έχει αποδειχθεί. είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  οπότε
οπότε  οπότε
οπότε  εγγράψιμο κλπ
εγγράψιμο κλπ οπότε
οπότε  άρα τα σημεία
άρα τα σημεία  θα είναι ομοκυκλικά δηλαδή και τα
θα είναι ομοκυκλικά δηλαδή και τα  αφού
αφού 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης