 ώστε:
ώστε:
Συντονιστές: cretanman, silouan, rek2
 , άρα
, άρα  , οπότε
, οπότε  άρτιος, έστω
άρτιος, έστω  ,
,  .
. .
.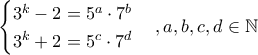 .
. , τότε
, τότε  και
και  , άτοπο.
, άτοπο. , τότε
, τότε  , άτοπο.
, άτοπο. .
.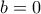 ή
ή  .
.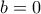 , πρέπει
, πρέπει  .
. , άτοπο, αφού
, άτοπο, αφού  .
. και το σύστημα γίνεται
και το σύστημα γίνεται  .
. .
. .
.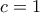 ,
,  , που είναι άτοπο από την προηγούμενη περίπτωση.
, που είναι άτοπο από την προηγούμενη περίπτωση. .
. .
. ,
,  .
. ,
,  , άτοπο.
, άτοπο.ΠανέμορφαΟρέστης Λιγνός έγραψε:Καλησπέρα Χάρη!
Πρέπει, άρα
, οπότε
άρτιος, έστω
,
.
Έτσι,.
Πρέπει λοιπόν.
Αν, τότε
και
, άτοπο.
Αν, τότε
, άτοπο.
Άρα,.
Με παρόμοια λογική πρέπειή
.
Αν, πρέπει
.
Έτσι,, άτοπο, αφού
.
Άρα,και το σύστημα γίνεται
.
Με αφαίρεση κατά μέλη.
Προφανώς,.
Αν,
, που είναι άτοπο από την προηγούμενη περίπτωση.
Άρα,.
Οπότε,.
Έχουμε,
.
Άρα,,
, άτοπο.
Ώστε, η αρχική εξίσωση είναι αδύνατη
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες