 τέτοιοι ώστε
τέτοιοι ώστε  .
.Συντονιστές: cretanman, silouan, rek2
Γράφουυμε
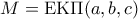 . Τότε έχουμε
. Τότε έχουμε  για κάποιους θετικούς ακεραίους
για κάποιους θετικούς ακεραίους  με
με 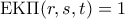 . Έχουμε
. Έχουμε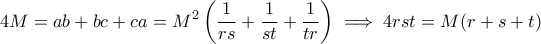
 τέτοιος, ώστε
τέτοιος, ώστε 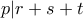 . Τότε
. Τότε 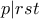 . Χωρίς βλάβη της γενικότητας
. Χωρίς βλάβη της γενικότητας 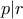 . Τότε
. Τότε 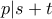 . Αν
. Αν 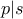 τότε
τότε 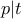 και επειδή
και επειδή 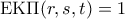 καταλήγουμε σε άτοπο. Άρα
καταλήγουμε σε άτοπο. Άρα 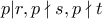 . Έστω
. Έστω  μέγιστο ώστε
μέγιστο ώστε 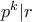 . Τότε
. Τότε  μέγιστο ώστε
μέγιστο ώστε 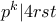 . Όμως
. Όμως  και έχουμε επίσης ότι
και έχουμε επίσης ότι 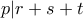 . Επομένως
. Επομένως 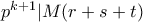 , άτοπο.
, άτοπο. 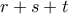 είναι δύναμη του
είναι δύναμη του  . Επειδή
. Επειδή 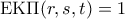 , δεν μπορούν τα
, δεν μπορούν τα  να είναι όλα άρτιοι. Αναγκαστικά θα έχουμε έναν άρτιο, έστω τον
να είναι όλα άρτιοι. Αναγκαστικά θα έχουμε έναν άρτιο, έστω τον  και δύο περιττός. Έστω
και δύο περιττός. Έστω  μέγιστο ώστε
μέγιστο ώστε 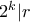 . Τότε έχουμε και
. Τότε έχουμε και 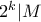 . Έχουμε επίσης ότι
. Έχουμε επίσης ότι 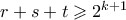 , άρα
, άρα 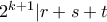 και
και 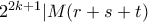 . Αφού
. Αφού 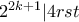 και
και 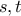 περιττοί, τότε
περιττοί, τότε 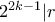 . Από τον ορισμό του
. Από τον ορισμό του  πρέπει
πρέπει 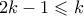 και αφού
και αφού  , τότε
, τότε  .
. 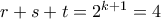 αφού αλλιώς θα είχαμε
αφού αλλιώς θα είχαμε 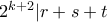 που θα κατέληγε σε άτοπο.
που θα κατέληγε σε άτοπο. 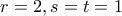 και προκύπτει
και προκύπτει 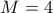 .
. 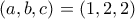 και οι μεταθέσεις της.
και οι μεταθέσεις της.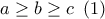 .
.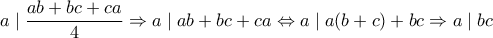
 ,
,  ,
,  διαιρεί τον
διαιρεί τον  , έπεται πως
, έπεται πως 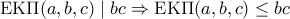
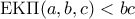 , τότε θα ήταν επίσης
, τότε θα ήταν επίσης 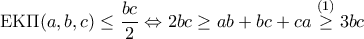 , ατοπο. Έτσι, είναι υποχρεωτικά
, ατοπο. Έτσι, είναι υποχρεωτικά 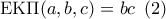 .
.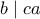 και κατόπιν
και κατόπιν 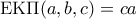 . Έτσι, προκύπτει
. Έτσι, προκύπτει 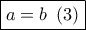 .
. , ομως, έχουμε:
, ομως, έχουμε: 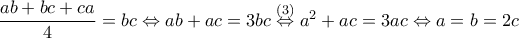 .
.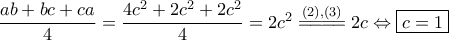 , απ' όπου
, απ' όπου 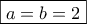 .
.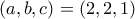 και οι αντιμεταθέσεις τους.
και οι αντιμεταθέσεις τους.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες