 φορές τότε να βρείτε το μέγιστο πλήθος σημείων τομής της «τεθλασμένης» με τα διάφορα κομμάτια της.
φορές τότε να βρείτε το μέγιστο πλήθος σημείων τομής της «τεθλασμένης» με τα διάφορα κομμάτια της.ΠΡΟΣΟΧΗ: Η άσκηση είναι δικής μου κατασκευής οπότε μπορεί να είναι μεγάλη πατάτα!
Συντονιστές: Demetres, socrates, silouan
 φορές τότε να βρείτε το μέγιστο πλήθος σημείων τομής της «τεθλασμένης» με τα διάφορα κομμάτια της.
φορές τότε να βρείτε το μέγιστο πλήθος σημείων τομής της «τεθλασμένης» με τα διάφορα κομμάτια της. ''αλλαγή κατεύθυνσης'', έχουμε
''αλλαγή κατεύθυνσης'', έχουμε  γραμμές.
γραμμές. ''αλλαγές κατεύθυνσης'', έχουμε
''αλλαγές κατεύθυνσης'', έχουμε  γραμμές.
γραμμές. αλλαγές ''κατεύθυνσης'', έχουμε
αλλαγές ''κατεύθυνσης'', έχουμε  γραμμές.
γραμμές. γραμμές που να συντρέχουν και ότι ανά δύο οι γραμμές δεν είναι παράλληλες.
γραμμές που να συντρέχουν και ότι ανά δύο οι γραμμές δεν είναι παράλληλες. (για
(για  ευθείες) (1).
ευθείες) (1). ευθείες, έχουμε το πολύ
ευθείες, έχουμε το πολύ  σημεία τομής.
σημεία τομής. -στη ευθεία τέμνει τις υπόλοιπες
-στη ευθεία τέμνει τις υπόλοιπες  σε
σε  σημεία.
σημεία. από αυτά, το σημείο όπου έγινε η τελευταία αλλαγή κατεύθυνσης.
από αυτά, το σημείο όπου έγινε η τελευταία αλλαγή κατεύθυνσης. σημεία τομής, συνολικά
σημεία τομής, συνολικά  ο.ε.δ.
ο.ε.δ. σημεία τομής.
σημεία τομής.Λίγο διαφορετικά:Ορέστης Λιγνός έγραψε:Γεια σου Χάρη!
Αν έχουμε''αλλαγή κατεύθυνσης'', έχουμε
γραμμές.
Αν έχουμε''αλλαγές κατεύθυνσης'', έχουμε
γραμμές.
Άρα, γενικά, γιααλλαγές ''κατεύθυνσης'', έχουμε
γραμμές.
Αφού θέλουμε το μέγιστο πλήθος σημείων τομής, υποθέτουμε ότι δεν υπάρχουνγραμμές που να συντρέχουν και ότι ανά δύο οι γραμμές δεν είναι παράλληλες.
Θα αποδείξουμε επαγωγικά ότι έχουμε το πολύ(για
ευθείες) (1).
Έστω ότι ισχύει η (1).
Θα αποδείξουμε λοιπόν ότι ισχύει το εξής: Αν έχουμεευθείες, έχουμε το πολύ
σημεία τομής.
Η-στη ευθεία τέμνει τις υπόλοιπες
σε
σημεία.
Όμως, πρέπει να αφαιρέσουμε τοαπό αυτά, το σημείο όπου έγινε η τελευταία αλλαγή κατεύθυνσης.
Άρα, έχουμεσημεία τομής, συνολικά
ο.ε.δ.
Άρα, έχουμε το πολύσημεία τομής.
 ευθύγραμμα τμήματα τέμνονται μεταξύ τους, άρα έχουμε
ευθύγραμμα τμήματα τέμνονται μεταξύ τους, άρα έχουμε 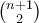 διαφορετικά ζευγάρια που δίνουν το πολύ
διαφορετικά ζευγάρια που δίνουν το πολύ  σημείο τομής. Επομένως έχουμε το πολύ
σημείο τομής. Επομένως έχουμε το πολύ  σημεία τομής (αφαιρούμε τα σημεία όπου απλώς άλλαξε η πορεία και δεν το θεωρούμε σημείο τομής).
σημεία τομής (αφαιρούμε τα σημεία όπου απλώς άλλαξε η πορεία και δεν το θεωρούμε σημείο τομής).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες