 με ίσο αριθμό ορθογωνίων
με ίσο αριθμό ορθογωνίων 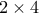 και
και 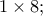
(Τα σχήματα μπορούν να περιστραφούν)
Συντονιστές: Demetres, socrates, silouan
 με ίσο αριθμό ορθογωνίων
με ίσο αριθμό ορθογωνίων 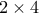 και
και 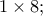
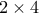 περιέχει
περιέχει  μαύρα και
μαύρα και  λευκά τετράγωνα.
λευκά τετράγωνα.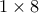 περιέχει
περιέχει  μαύρα και
μαύρα και  λευκά τετράγωνα.
λευκά τετράγωνα.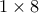 είναι μονόχρωμο.
είναι μονόχρωμο.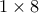 που βρίσκονται σε άρτιες στήλες να είναι με το πλήθος των κάθετων
που βρίσκονται σε άρτιες στήλες να είναι με το πλήθος των κάθετων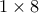 που βρίσκονται σε περιττές στήλες.
που βρίσκονται σε περιττές στήλες.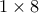 είναι άρτιο.
είναι άρτιο.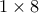 είναι άρτιο.
είναι άρτιο.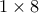 είναι άρτιο αδύνατο αφού ισούται με
είναι άρτιο αδύνατο αφού ισούται με 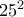 .
. που είναι τέτοιοι ώστε να είναι δυνατόν να καλύψουμε σκακιέρα
που είναι τέτοιοι ώστε να είναι δυνατόν να καλύψουμε σκακιέρα  με ίσο αριθμό ορθογωνίων
με ίσο αριθμό ορθογωνίων 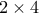 και
και 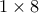
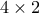 ή
ή 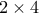 πλακιδίων είναι περιττό.
πλακιδίων είναι περιττό. μια (οποιαδήποτε) πρωταρχική όγδοη ρίζα της μονάδας (που ταυτίζεται με τις ρίζες του πολυωνύμου
μια (οποιαδήποτε) πρωταρχική όγδοη ρίζα της μονάδας (που ταυτίζεται με τις ρίζες του πολυωνύμου 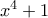 ).
). τον αριθμό
τον αριθμό 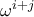 .
.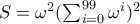 το οποίο από τη σχέση
το οποίο από τη σχέση 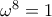 κάνει
κάνει 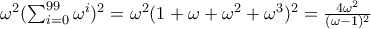 .
. πλακιδίων στο παραπάνω άθροισμα είναι μηδενική, ενώ κάθε
πλακιδίων στο παραπάνω άθροισμα είναι μηδενική, ενώ κάθε  ή
ή 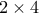 πλακίδιο συνεισφέρει κατά
πλακίδιο συνεισφέρει κατά 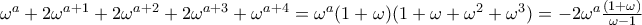 όπου
όπου  το άθροισμα των συντεταγμένων του πάνω αριστερά πλακιδίου του ορθογωνίου αυτού.
το άθροισμα των συντεταγμένων του πάνω αριστερά πλακιδίου του ορθογωνίου αυτού. βάσει του αθροίσματος των συνεισφορών των πλακιδίων) παίρνουμε την ισότητα
βάσει του αθροίσματος των συνεισφορών των πλακιδίων) παίρνουμε την ισότητα 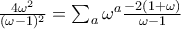 όπου το άθροισμα στο δεξί μέλος είναι πάνω από περιττό αριθμό α/πλακιδίων λόγω της υπόθεσης.
όπου το άθροισμα στο δεξί μέλος είναι πάνω από περιττό αριθμό α/πλακιδίων λόγω της υπόθεσης.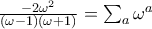 από όπου πολλαπλασιάζοντας αριθμητή και παρονομαστή με
από όπου πολλαπλασιάζοντας αριθμητή και παρονομαστή με 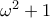 και λόγω της
και λόγω της 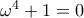 προκύπτει
προκύπτει 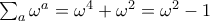 .
. (διότι
(διότι 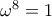 ) καθώς και
) καθώς και  μόνο που τότε κάθε αναγωγή συνοδεύεται από αλλαγή προσήμου. Έτσι καταλήγουμε σε σχέση της μορφής
μόνο που τότε κάθε αναγωγή συνοδεύεται από αλλαγή προσήμου. Έτσι καταλήγουμε σε σχέση της μορφής 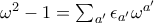 όπου τα
όπου τα 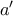 στο δεξί μέλος είναι περιττά το πλήθος, δεν υπερβαίνουν το 4, και
στο δεξί μέλος είναι περιττά το πλήθος, δεν υπερβαίνουν το 4, και 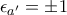 .
.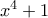 και επομένως ισχύει ταυτοτικά ως ισότητα πολυωνύμων.
και επομένως ισχύει ταυτοτικά ως ισότητα πολυωνύμων.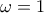 στα 2 μέλη, το ένα αριστερό μέλος είναι άρτιο και το δεξί περιττό, άτοπο.
στα 2 μέλη, το ένα αριστερό μέλος είναι άρτιο και το δεξί περιττό, άτοπο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες