 , δεν αποτελούν πυθαγόρεια τριάδα.
, δεν αποτελούν πυθαγόρεια τριάδα.Φιλικά.
Συντονιστές: achilleas, emouroukos, silouan
 , δεν αποτελούν πυθαγόρεια τριάδα.
, δεν αποτελούν πυθαγόρεια τριάδα. . Άρα το τελευταίο ψηφίο του δοσμένου αριθμού πρέπει να είναι ένα από αυτά. Όμως ο αριθμός ισούται με
. Άρα το τελευταίο ψηφίο του δοσμένου αριθμού πρέπει να είναι ένα από αυτά. Όμως ο αριθμός ισούται με  σε περιττή δύναμη και άρα το τελευταίο ψηφίο του πρέπει να ισούται με
σε περιττή δύναμη και άρα το τελευταίο ψηφίο του πρέπει να ισούται με  ή
ή  , άτοπο.
, άτοπο.Πολύ όμορφα κ. Δημήτρη! Ας το συνεχίσουμε. Να βρεθούν ταDemetres έγραψε:Η μόνη πυθαγόρεια τριάδα με μονοψήφιους αριθμούς είναι η. Άρα το τελευταίο ψηφίο του δοσμένου αριθμού πρέπει να είναι ένα από αυτά. Όμως ο αριθμός ισούται με
σε περιττή δύναμη και άρα το τελευταίο ψηφίο του πρέπει να ισούται με
ή
, άτοπο.
 τελευταία ψηφία του αριθμού αυτού.
τελευταία ψηφία του αριθμού αυτού.Ας το δούμε γιατί έχει πλάκαM.S.Vovos έγραψε: ↑Σάβ Μαρ 25, 2017 5:01 pmΠολύ όμορφα κ. Δημήτρη! Ας το συνεχίσουμε. Να βρεθούν ταDemetres έγραψε:Η μόνη πυθαγόρεια τριάδα με μονοψήφιους αριθμούς είναι η. Άρα το τελευταίο ψηφίο του δοσμένου αριθμού πρέπει να είναι ένα από αυτά. Όμως ο αριθμός ισούται με
σε περιττή δύναμη και άρα το τελευταίο ψηφίο του πρέπει να ισούται με
ή
, άτοπο.
τελευταία ψηφία του αριθμού αυτού.
Φιλικά.
 .Είναι
.Είναι 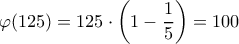 για αυτό θα βρω το
για αυτό θα βρω το  .Είναι
.Είναι  οπότε θα βρω το
οπότε θα βρω το 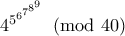 .Θέτω
.Θέτω 
 .Έστω
.Έστω  .Πρέπει
.Πρέπει  άρα με δοκιμές είναι
άρα με δοκιμές είναι  ,έστω
,έστω  .Τότε θα είναι
.Τότε θα είναι 
 τότε
τότε  .
. τότε
τότε 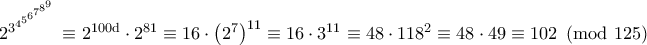
 .Είναι
.Είναι  .Επειδή προφανώς
.Επειδή προφανώς  θα είναι
θα είναι  η οποία με δοκιμές δίνει
η οποία με δοκιμές δίνει  .Θέτω
.Θέτω 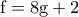 .
.
 είναι το
είναι το 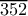 .
. δεν μπορεί να χρησιμοποιηθεί το Euler-Fermat για το
δεν μπορεί να χρησιμοποιηθεί το Euler-Fermat για το  . Βγαίνει βέβαια άμεσα ότι
. Βγαίνει βέβαια άμεσα ότι  .
.Έχετε δίκιο κύριε Δημήτρη,ευτυχώς διορθώνεται εύκολα.Υπάρχουν και άλλα λάθη στην λύση μου,τα διορθώνω.(πάντως καταλήγει στο ίδιο αποτέλεσμα
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες