 και άθροισμα τετραγώνων
και άθροισμα τετραγώνων  .
.Βρείτε τη μέγιστη και την ελάχιστη τιμή του καθένα τους ,καθώς επίσης και
τους υπόλοιπους τρείς στην κάθε μία από τις δύο περιπτώσεις .
Συντονιστές: achilleas, emouroukos, silouan
 και άθροισμα τετραγώνων
και άθροισμα τετραγώνων  .
. τον έναν απ'αυτούς , τότε η μέγιστη τιμή του
τον έναν απ'αυτούς , τότε η μέγιστη τιμή του  είναι
είναι  ,
, . Η ελάχιστη τιμή του
. Η ελάχιστη τιμή του 
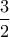 , οπότε οι άλλοι τρείς είναι οι :
, οπότε οι άλλοι τρείς είναι οι :  .
.Εχω αντίθετη άποψη Θανάση.
 ένας από αυτούς και
ένας από αυτούς και  οι άλλοι.
οι άλλοι.


 και ελάχιστη το
και ελάχιστη το 
 η C-S για τα
η C-S για τα  δίνει ισότητα και βρίσκουμε αυτά που γράφει ο Θανάσης.
δίνει ισότητα και βρίσκουμε αυτά που γράφει ο Θανάσης.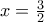
 , με την εξής εκφώνηση :
, με την εξής εκφώνηση : , ικανοποιούν τις :
, ικανοποιούν τις : 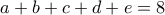 και
και  , βρείτε την μέγιστη και την ελάχιστη τιμή του
, βρείτε την μέγιστη και την ελάχιστη τιμή του  .
. ,
, , που βέβαια ( τετραγωνίζοντας ) καταλήγει
, που βέβαια ( τετραγωνίζοντας ) καταλήγει 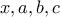 είναι οι αριθμοί μας , τότε
είναι οι αριθμοί μας , τότε  θα είναι
θα είναι  , συνεπώς υπάρχουν πραγματικοί
, συνεπώς υπάρχουν πραγματικοί  , ώστε :
, ώστε :  και
και  , επομένως :
, επομένως : , που γίνεται :
, που γίνεται :  και δίνει :
και δίνει :  κ.λ.π.
κ.λ.π. πραγματικοί.
πραγματικοί.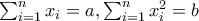
 τότε να βρεθούν
τότε να βρεθούν 


 ,
,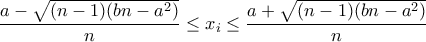


Να τα κάνω πιο λιανά. Αν στην Στατιστική έχουμε ένα δείγμα(παρατηρήσεις) τότε τοΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Οκτ 25, 2017 3:47 pmΤο ξεφτιλίσαμε.
Βλέπω ότι το πρόβλημα έχει σχέση με Στατιστική.
Γιατί το
εχει σχέση με την μέση τιμή
ενώ το
με την διασπορά.
Φτάνει.


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες