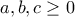 με
με  , να αποδειχθεί ότι
, να αποδειχθεί ότι 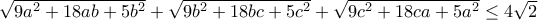
(Κάνει και για Juniors)
Συντονιστές: achilleas, emouroukos, silouan
Παρατηρώ πως
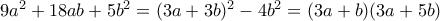 , επομένως με βάση την ανισότητα
, επομένως με βάση την ανισότητα 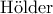 :
: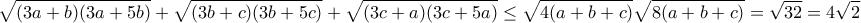
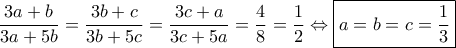
.
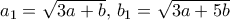 , και λοιπά.
, και λοιπά.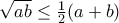 , συν ένα μικρό κόλπο στο σημείο
, συν ένα μικρό κόλπο στο σημείο  .
. 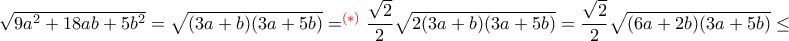
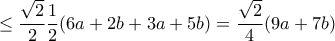 , και όμοια οι άλλες δύο.
, και όμοια οι άλλες δύο. 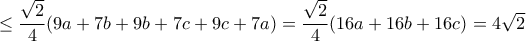 με ισότητα όταν
με ισότητα όταν  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες