 θετικοί αριθμοί, να αποδειχθεί ότι
θετικοί αριθμοί, να αποδειχθεί ότι 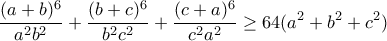
(κάνει και για καλούς Junior)
Συντονιστές: achilleas, emouroukos, silouan
 θετικοί αριθμοί, να αποδειχθεί ότι
θετικοί αριθμοί, να αποδειχθεί ότι 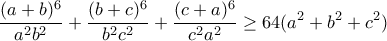
Θα αποδείξουμε ότιMihalis_Lambrou έγραψε: ↑Σάβ Οκτ 21, 2023 9:53 amΑνθετικοί αριθμοί, να αποδειχθεί ότι
(κάνει και για καλούς Junior)
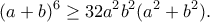 Με πρόσθεση κατά μέλη της όμοιας με αυτήν, παίρνουμε το ζητούμενο.
Με πρόσθεση κατά μέλη της όμοιας με αυτήν, παίρνουμε το ζητούμενο.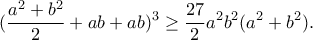
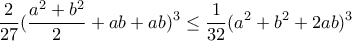 που είναι ισοδύναμη με
που είναι ισοδύναμη με 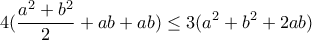 που καταλήγει στην
που καταλήγει στην 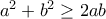 , που ισχύει.
, που ισχύει.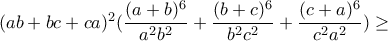
![\left [ (a+b)^2+(b+c)^2+(c+a)^2 \right ]^3=8(a^2+b^2+c^2+ab+bc+ca)^3 \left [ (a+b)^2+(b+c)^2+(c+a)^2 \right ]^3=8(a^2+b^2+c^2+ab+bc+ca)^3](/forum/ext/geomar/texintegr/latexrender/pictures/615c8dc2218fb51f32d0c813e76fc2c2.png) .
.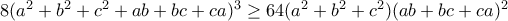 .
.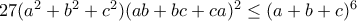 ,
,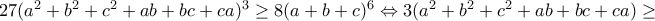
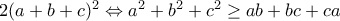 ,
,Αυτό που είχα κατά νου: Θα αποδείξουμε πρώτα
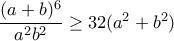 και κυκλικά (όπως δηλαδή το πρώτο βήμα στην λύση του Σιλουανού) και μετά προσθέτουμε τις τρεις κατά μέλη.
και κυκλικά (όπως δηλαδή το πρώτο βήμα στην λύση του Σιλουανού) και μετά προσθέτουμε τις τρεις κατά μέλη. 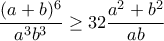 ή αλλιώς
ή αλλιώς 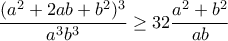 , με άλλα λόγια θέλουμε
, με άλλα λόγια θέλουμε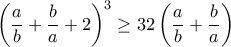 .
. 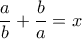 , έχουμε
, έχουμε  και το αποδεικτέο γίνεται
και το αποδεικτέο γίνεται 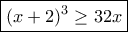 . Αυτό είναι άμεσο:
. Αυτό είναι άμεσο: 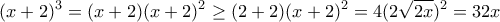 , όπως θέλαμε.
, όπως θέλαμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες