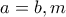 , όπου
, όπου  ακέραιος μεγαλύτερος του
ακέραιος μεγαλύτερος του  και
και  μονοψήφιος φυσικός αριθμός.
μονοψήφιος φυσικός αριθμός.Να βρεθούν όλες οι δυνατές τιμές του
 , ώστε η ανίσωση:
, ώστε η ανίσωση: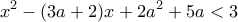
να έχει ακριβώς
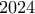 ακέραιες λύσεις.
ακέραιες λύσεις.Συντονιστές: achilleas, emouroukos, silouan
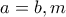 , όπου
, όπου  ακέραιος μεγαλύτερος του
ακέραιος μεγαλύτερος του  και
και  μονοψήφιος φυσικός αριθμός.
μονοψήφιος φυσικός αριθμός. , ώστε η ανίσωση:
, ώστε η ανίσωση: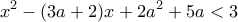
 ακέραιες λύσεις.
ακέραιες λύσεις.Το τριώνυμοΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε: ↑Κυρ Φεβ 25, 2024 5:36 pmΘεωρούμε τον δεκαδικό αριθμό, όπου
ακέραιος μεγαλύτερος του
και
μονοψήφιος φυσικός αριθμός.
Να βρεθούν όλες οι δυνατές τιμές του, ώστε η ανίσωση:
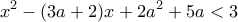
να έχει ακριβώςακέραιες λύσεις.
 έχει ρίζες τις
έχει ρίζες τις 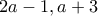 , με "απόσταση"
, με "απόσταση" 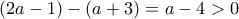 και είναι αρνητικό, όπως θέλουμε, μεταξύ των ριζών του.
και είναι αρνητικό, όπως θέλουμε, μεταξύ των ριζών του. για τις οποίες μεταξύ των αριθμών
για τις οποίες μεταξύ των αριθμών 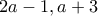 υπάρχουν
υπάρχουν  ακέραιοι αριθμοί.
ακέραιοι αριθμοί.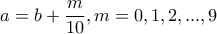 έχουμε τις παρακάτω περιπτώσεις:
έχουμε τις παρακάτω περιπτώσεις: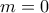 , τότε μεταξύ των ριζών υπάρχουν
, τότε μεταξύ των ριζών υπάρχουν 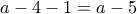 ακέραιοι και θα πρέπει:
ακέραιοι και θα πρέπει: 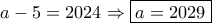
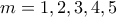 τότε μεταξύ των ριζών υπάρχουν
τότε μεταξύ των ριζών υπάρχουν  ακέραιοι και θα πρέπει:
ακέραιοι και θα πρέπει: 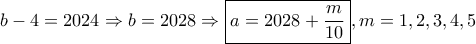
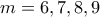 τότε μεταξύ των ριζών υπάρχουν
τότε μεταξύ των ριζών υπάρχουν 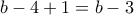 ακέραιοι και θα πρέπει:
ακέραιοι και θα πρέπει: 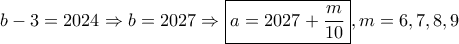
 !
!

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες