 τριγώνου
τριγώνου  τέμνει τον περιγγεγραμμένο κύκλο του τριγώνου
τέμνει τον περιγγεγραμμένο κύκλο του τριγώνου στο
 . Έστω
. Έστω  η προβολή του
η προβολή του  στη
στη  και
και  η τομή με την
η τομή με την  της
της παράλληλης από το
 στη
στη  . Δείξετε ότι
. Δείξετε ότι  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 τριγώνου
τριγώνου  τέμνει τον περιγγεγραμμένο κύκλο του τριγώνου
τέμνει τον περιγγεγραμμένο κύκλο του τριγώνου  . Έστω
. Έστω  η προβολή του
η προβολή του  στη
στη  και
και  η τομή με την
η τομή με την  της
της  στη
στη  . Δείξετε ότι
. Δείξετε ότι  .
.ΈστωDoloros έγραψε:Τ
Η διχοτόμοςτριγώνου
τέμνει τον περιγγεγραμμένο κύκλο του τριγώνου στο
. Έστω
η προβολή του
στη
και
η τομή με την
της παράλληλης από το
στη
. Δείξετε ότι
.
 το σημείο τομής του περίκυκλου του τριγώνου
το σημείο τομής του περίκυκλου του τριγώνου  με την
με την  . Τότε
. Τότε 
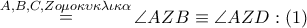 και
και  .
.

 το μέσο της
το μέσο της  .
.
 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.ΑφούDoloros έγραψε:Ωραία ο Κ. Στάθης
Πάντως αναμένω τουλάχιστον μια ακόμη λύση .
Φιλικά, Νίκος
 ,
,  (από το Θ. διχοτόμων).
(από το Θ. διχοτόμων). παίρνουμε σημείο
παίρνουμε σημείο  ώστε
ώστε  .
.  αφού έχουν
αφού έχουν  με συνέπεια
με συνέπεια  .
. είναι εγγεγραμμένο άρα
είναι εγγεγραμμένο άρα  , δηλαδή το
, δηλαδή το  είναι ισοσκελές και το
είναι ισοσκελές και το  είναι μέσο του
είναι μέσο του  .
. .
. έχουν κοινή την γωνία
έχουν κοινή την γωνία  , οπότε:
, οπότε:  .
. στηριζόταν η φράση , περιμένω
στηριζόταν η φράση , περιμένω  .
. θα είναι
θα είναι  .Αν
.Αν  η προβολή του
η προβολή του 
 τα ορθογώνια τρίγωνα
τα ορθογώνια τρίγωνα  έχουν
έχουν  οπότε είναι ίσα και άρα
οπότε είναι ίσα και άρα  . έτσι
. έτσι  .
.  το ύψος του
το ύψος του  και
και  θα ισχύουν :
θα ισχύουν :
 και λόγω των
και λόγω των  δίδει :
δίδει :  ,
,Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες