 η διάμεσος
η διάμεσος  είναι σταθερή κατά θέση και μέγεθος, ενώ οι κορυφές
είναι σταθερή κατά θέση και μέγεθος, ενώ οι κορυφές 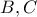 κινούνται έτσι ώστε
κινούνται έτσι ώστετο μήκος της πλευράς
 να παραμένει σταθερό. Να βρείτε το γεωμετρικό τόπο του ορθοκέντρου
να παραμένει σταθερό. Να βρείτε το γεωμετρικό τόπο του ορθοκέντρου  του τριγώνου
του τριγώνου 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 η διάμεσος
η διάμεσος  είναι σταθερή κατά θέση και μέγεθος, ενώ οι κορυφές
είναι σταθερή κατά θέση και μέγεθος, ενώ οι κορυφές 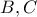 κινούνται έτσι ώστε
κινούνται έτσι ώστε να παραμένει σταθερό. Να βρείτε το γεωμετρικό τόπο του ορθοκέντρου
να παραμένει σταθερό. Να βρείτε το γεωμετρικό τόπο του ορθοκέντρου  του τριγώνου
του τριγώνου 
 η προβολή του ορθοκέντρου
η προβολή του ορθοκέντρου  στον φορέα της διαμέσου
στον φορέα της διαμέσου  , Από το εγγράψιμμο
, Από το εγγράψιμμο 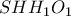 έχουμε ότι
έχουμε ότι  (1)
(1)
 είναι το μήκος των ίσων τμημάτων
είναι το μήκος των ίσων τμημάτων  και
και  . Αλλά:
. Αλλά:
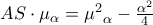
 , άρα και το
, άρα και το  είναι σταθερό. Επομένως το ορθόκεντρο ανήκει σε σταθερή ευθεία κάθετη στην σταθερή διάμεσο στο
είναι σταθερό. Επομένως το ορθόκεντρο ανήκει σε σταθερή ευθεία κάθετη στην σταθερή διάμεσο στο  .
. της ευθείας αυτής διάφορο του
της ευθείας αυτής διάφορο του  κατασκευάζονται διαδοχικά το
κατασκευάζονται διαδοχικά το  , ο φορέας της πλευράς
, ο φορέας της πλευράς  , η ευθεία Euler, το κέντρο του περιγργραμμένου κύκλου και τέλος οι κορυφές
, η ευθεία Euler, το κέντρο του περιγργραμμένου κύκλου και τέλος οι κορυφές  και επομένως ο τόπος είναι η συγκεκριμένη ευθεία. Δεν γράφω διερεύνηση γιατί είναι περασμένη η ώρα.
και επομένως ο τόπος είναι η συγκεκριμένη ευθεία. Δεν γράφω διερεύνηση γιατί είναι περασμένη η ώρα.Γιώργο και Νίκο καλημέρα!. Είναι προφανές (λεπτομέρειες αύριο γιατί ακόμα και στις βρυξέλλες (με μια ώρα νωρίτερα είναι αργάgeorge visvikis έγραψε:Σε οξυγώνιο τρίγωνοη διάμεσος
είναι σταθερή κατά θέση και μέγεθος, ενώ οι κορυφές
κινούνται έτσι ώστε
το μήκος της πλευράςνα παραμένει σταθερό. Να βρείτε το γεωμετρικό τόπο του ορθοκέντρου
του τριγώνου
 και του κύκλου διαμέτρου
και του κύκλου διαμέτρου 
Έστωgeorge visvikis έγραψε:Σε οξυγώνιο τρίγωνοη διάμεσος
είναι σταθερή κατά θέση και μέγεθος, ενώ οι κορυφές
κινούνται έτσι ώστε το μήκος της πλευράς
να παραμένει σταθερό. Να βρείτε το γεωμετρικό τόπο του ορθοκέντρου
του τριγώνου
 , με
, με  διάμεσος (σταθερή κατά μέτρο και θέση) και
διάμεσος (σταθερή κατά μέτρο και θέση) και  σταθερή μόνο κατά μέτρο, και
σταθερή μόνο κατά μέτρο, και  , όπου
, όπου  η κοινή χορδή των σταθερών κύκλων
η κοινή χορδή των σταθερών κύκλων  και του κύκλου
και του κύκλου  διαμέτρου
διαμέτρου  .
. (Σχήμα 1) Έστω
(Σχήμα 1) Έστω  το ορθόκεντρο του τριγώνου
το ορθόκεντρο του τριγώνου  . Αν
. Αν  τα ύψη του
τα ύψη του  προφανώς
προφανώς  (αφού
(αφού 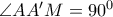 ) και
) και  (αφού
(αφού  ) .
) . 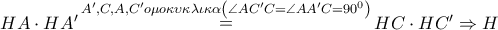 έχει ίσες δυνάμεις ως προς του κύκλου
έχει ίσες δυνάμεις ως προς του κύκλου  και συνεπώς είναι σημείο του ριζικούς τους άξονα
και συνεπώς είναι σημείο του ριζικούς τους άξονα  με
με 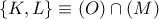 , άρα
, άρα  .
. (Σχήμα 2) Έστω
(Σχήμα 2) Έστω  και θα δείξουμε ότι το
και θα δείξουμε ότι το  είναι ορθόκεντρο τριγώνου
είναι ορθόκεντρο τριγώνου  με τις προδιαγραφές της εκφώνησης.
με τις προδιαγραφές της εκφώνησης.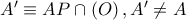 και
και  διάμετρος του κύκλου
διάμετρος του κύκλου 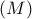 διερχόμενη από το
διερχόμενη από το  . Τότε
. Τότε  (αφού
(αφού  διάμετρος του
διάμετρος του  ) , δηλαδή το
) , δηλαδή το  είναι σημείο του ύψους
είναι σημείο του ύψους 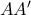 του εν λόγω τριγώνου
του εν λόγω τριγώνου  . Προφανώς
. Προφανώς  (διάκεντρος κάθετη στο ριζικό άξονα κύκλων και ας είναι
(διάκεντρος κάθετη στο ριζικό άξονα κύκλων και ας είναι  .
.  διάμετρο του
διάμετρο του  εφαπτόμενη του
εφαπτόμενη του  , όπου
, όπου  .
. 

 ομοκυκλικά και με
ομοκυκλικά και με 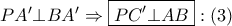 .
.  (αφού
(αφού  διάμετρος του
διάμετρος του 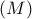 . Από
. Από 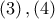 προκύπτει ότι
προκύπτει ότι  συνευθειακά (σε σημείο ευθείας υψώνεται μοναδική κάθετη σε αυτή) δηλαδή το
συνευθειακά (σε σημείο ευθείας υψώνεται μοναδική κάθετη σε αυτή) δηλαδή το  είναι σημείο και του ύψους (εκτός του
είναι σημείο και του ύψους (εκτός του 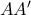 )
)  του τριγώνου
του τριγώνου  και άρα είναι το ορθόκεντρό του, δηλαδή
και άρα είναι το ορθόκεντρό του, δηλαδή  .
. .
. θέλουμε να είναι οξυγώνιο ο ζητούμενος γεωμετρικός τόπος περιορίζεται (προφανώς) στην κοινή χορδή
θέλουμε να είναι οξυγώνιο ο ζητούμενος γεωμετρικός τόπος περιορίζεται (προφανώς) στην κοινή χορδή  των κύκλων
των κύκλων  χωρίς τα άκρα της
χωρίς τα άκρα της 
 την προβολή του κέντρου του περιγεγραμμένου κύκλου στην διάμεσο και με
την προβολή του κέντρου του περιγεγραμμένου κύκλου στην διάμεσο και με  το σημείο τομής του φορέα της με τον κύκλο.
το σημείο τομής του φορέα της με τον κύκλο.  βγαίνει σταθερό οπότε το μέσο
βγαίνει σταθερό οπότε το μέσο  του
του  είναι σταθερό. Άρα το
είναι σταθερό. Άρα το  ανήκει σε σταθερή ευθεία επομένως και το ομοιόθετο του
ανήκει σε σταθερή ευθεία επομένως και το ομοιόθετο του  ως προς κέντρο ομοιοθεσίας το σταθερό
ως προς κέντρο ομοιοθεσίας το σταθερό  . Τ
. ΤΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες