a) Αν

η προβολή του

στην

, τότε η πολική του

ως προς τις ευθείες

είναι η ευθεία
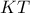
. Η ευθεία

διέρχεται από τα μέσα των
Βάσεων

των βάσεων

του τραπεζίου

έτσι τα σημεία

αποτελούν αρμονική σημειοσειρά, οπότε και τα σημεία

αποτελούν αρμονική σημειοσειρά και αφού

το τμήμα

είναι
εφαπτόμενο του ημικυκλίου .

- Στρυφνό τμήμα.png (24.13 KiB) Προβλήθηκε 369 φορές
b) Αν

το συμμετρικό του

ως προς

ο κύκλος διαμέτρου

είναι
εγγεγραμμένος στο
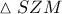
. Το τρίγωνο αυτό έχει ημιπερίμετρο

αν λοιπόν θέσω

θα έχω:

οπότε και λόγω της

έχω :

και προκύπτει η εξίσωση :
![{b^2}{(2y + d)^2} = {d^2}[{b^2} + 4{(y + d)^2}] {b^2}{(2y + d)^2} = {d^2}[{b^2} + 4{(y + d)^2}]](/forum/ext/geomar/texintegr/latexrender/pictures/4a1ef14e8c2b95675f69c821fa096304.png)
με δεκτή λύση :
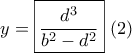
.
Επειδή δε

λόγω της

έχω:

. π. χ. με

προκύπτει το επαληθευμένο αποτέλεσμα :
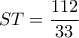
.
 . Στην εφαπτομένη του στο
. Στην εφαπτομένη του στο  , ορίσαμε σημείο
, ορίσαμε σημείο  ,
, . Η
. Η  τέμνει το τόξο στο
τέμνει το τόξο στο  , ενώ η
, ενώ η  τέμνει την άλλη
τέμνει την άλλη , στο σημείο
, στο σημείο  . Οι προεκτάσεις των
. Οι προεκτάσεις των  τέμνονται στο
τέμνονται στο  .
. εφάπτεται του ημικυκλίου ... β) Υπολογίστε το
εφάπτεται του ημικυκλίου ... β) Υπολογίστε το  .
. . Πρέπει να βρείτε :
. Πρέπει να βρείτε : 

 στο
στο  .
.
 .
. (1).
(1). έχουμε
έχουμε  .
. , οπότε
, οπότε  .
. είναι εφαπτόμενο τμήμα, και αφού
είναι εφαπτόμενο τμήμα, και αφού  , το
, το 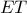 είναι επίσης εφαπτόμενο τμήμα, δηλαδή η
είναι επίσης εφαπτόμενο τμήμα, δηλαδή η  , η
, η  (2).
(2).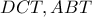 είναι όμοια, οπότε
είναι όμοια, οπότε 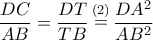 .
. (3).
(3). είναι
είναι  (4).
(4). .
. .
. , και για την εφαρμογή,
, και για την εφαρμογή,  .
. η προβολή του
η προβολή του  , τότε η πολική του
, τότε η πολική του  είναι η ευθεία
είναι η ευθεία 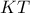 . Η ευθεία
. Η ευθεία  των βάσεων
των βάσεων  του τραπεζίου
του τραπεζίου  έτσι τα σημεία
έτσι τα σημεία  αποτελούν αρμονική σημειοσειρά, οπότε και τα σημεία
αποτελούν αρμονική σημειοσειρά, οπότε και τα σημεία 
 το τμήμα
το τμήμα  το συμμετρικό του
το συμμετρικό του  ως προς
ως προς  . Το τρίγωνο αυτό έχει ημιπερίμετρο
. Το τρίγωνο αυτό έχει ημιπερίμετρο  αν λοιπόν θέσω
αν λοιπόν θέσω  θα έχω:
θα έχω:  οπότε και λόγω της
οπότε και λόγω της  έχω :
έχω : και προκύπτει η εξίσωση :
και προκύπτει η εξίσωση : ![{b^2}{(2y + d)^2} = {d^2}[{b^2} + 4{(y + d)^2}] {b^2}{(2y + d)^2} = {d^2}[{b^2} + 4{(y + d)^2}]](/forum/ext/geomar/texintegr/latexrender/pictures/4a1ef14e8c2b95675f69c821fa096304.png) με δεκτή λύση :
με δεκτή λύση : 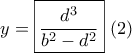 .
. λόγω της
λόγω της  έχω:
έχω:  . π. χ. με
. π. χ. με  προκύπτει το επαληθευμένο αποτέλεσμα :
προκύπτει το επαληθευμένο αποτέλεσμα : 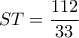 .
.