Στο ημικύκλιο
Δημοσιεύτηκε: Δευ Απρ 17, 2017 12:49 pm
Έστω ημικύκλιο διαμέτρου  και κέντρου
και κέντρου  . Ας είναι
. Ας είναι  το μέσο του
το μέσο του 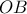 .
.
Σημείο διατρέχει τα εσωτερικά σημεία της ακτίνας
διατρέχει τα εσωτερικά σημεία της ακτίνας  .
.
1. Να βρεθεί σημείο στο ημικύκλιο τέτοιο ώστε αν η
στο ημικύκλιο τέτοιο ώστε αν η  τέμνει , ακόμα,
τέμνει , ακόμα,
τον κύκλο στο
στο  να είναι
να είναι 
2. Να βρεθούν οι θέσεις του για τις οποίες
για τις οποίες
a)
b)
 και κέντρου
και κέντρου  . Ας είναι
. Ας είναι  το μέσο του
το μέσο του 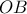 .
. Σημείο
 διατρέχει τα εσωτερικά σημεία της ακτίνας
διατρέχει τα εσωτερικά σημεία της ακτίνας  .
. 1. Να βρεθεί σημείο
 στο ημικύκλιο τέτοιο ώστε αν η
στο ημικύκλιο τέτοιο ώστε αν η  τέμνει , ακόμα,
τέμνει , ακόμα, τον κύκλο
 στο
στο  να είναι
να είναι 
2. Να βρεθούν οι θέσεις του
 για τις οποίες
για τις οποίες a)

b)

 , τότε από το θεώρημα των τεμνομένων χορδών στον κύκλο
, τότε από το θεώρημα των τεμνομένων χορδών στον κύκλο  θα ισχύει:
θα ισχύει: 
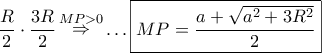
 θα έχουμε:
θα έχουμε: 






