 είναι το μέσο του ημικυκλίου διαμέτρου
είναι το μέσο του ημικυκλίου διαμέτρου  και το
και το  σημείο
σημείοτης προέκτασης της
 . Η ευθεία
. Η ευθεία  τέμνει το τόξο στο σημείο
τέμνει το τόξο στο σημείο  .
. Η εφαπτομένη του ημικυκλίου στο
 , τέμνει την
, τέμνει την  στο σημείο
στο σημείο  .
.α) Δείξτε ότι
 .... β) Αν
.... β) Αν  , υπολογίστε το
, υπολογίστε το  .
.
 το κέντρο του ημικυκλίου. Παρατηρούμε ότι
το κέντρο του ημικυκλίου. Παρατηρούμε ότι 
 , άρα
, άρα  ισοσκελές. Επίσης από Δύναμη Σημείου έχουμε
ισοσκελές. Επίσης από Δύναμη Σημείου έχουμε . Άρα
. Άρα  .
. 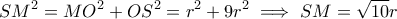 . Πάλι με Δύναμη Σημείου
. Πάλι με Δύναμη Σημείου  . Έστω
. Έστω  . Ισχύει
. Ισχύει  .
.  .
. η προβολή του
η προβολή του  . Έχω
. Έχω  ως εξωτερική στο
ως εξωτερική στο  . Επίσης
. Επίσης 

 και η
και η  εφαπτομένη του ημικυκλίου )
εφαπτομένη του ημικυκλίου )  λόγω μεταβατικότητας έχω
λόγω μεταβατικότητας έχω 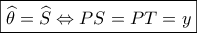 .
.
 . Έτσι θα έχω :
. Έτσι θα έχω : 
 και
και  .
.