Ὑπολογισμὸς ἐμβαδοῦ ἐξαγώνου

Γ.-Σ. Σμυρλής · #1

Δίδεται ἑξάγωνο ΑΒΓΔΕΖ τοῦ ὁποίου ὅλες οἱ πλευρὲς εἶναι ἴσες, καὶ τὰ ζεύγη ἀπέναντι πλευρῶν παράλληλα. Δηλαδὴ, ΑΒ $\parallel$ ΔΕ, ΒΓ $\parallel$ ΕΖ καὶ ΓΔ $\parallel$ ΕΖ. Ἐπίσης, οἱ ἀποστάσεις τῶν παραλλήλων πλευρῶν εἶναι 7,8 καὶ 9, ἀντιστοίχως.

Νὰ ὑπολογισθεῖ τὸ ἐμβαδὸν τοῦ ἑξαγώνου.

KARKAR · #2

: Εξάγωνο.png (34.11 KiB) Προβλήθηκε 543 φορές

. Είναι απλό από ομοιότητα τριγώνων να διαπιστωθεί ότι ET=7

Γ.-Σ. Σμυρλής · #3

Πράγματι ἡ ἀπάντηση εἶναι 50.

Ὑπάρχει ὅμως ἔκφραση τοῦ ἐμβαδοῦ συναρτήσει τῶν d_1,d_2

καὶ

;

Γ.-Σ. Σμυρλής · #4

Δίδω τὴν ἀπάντηση, χωρὶς τὴν ἀπόδειξη:
$\displaystyle{ E=\frac{1}{2}r(d_1+d_2+d_3), }$
ὅπου

ἡ πλευρὰ τοῦ ἑξαγώνου, ἡ ὁποία δίδεται, συναρτήσει τῶν d_1,d_2

καὶ

, ἀπὸ τὸν τύπο
$\displaystyle{ r=\frac{xyz}{\sqrt{2x^2y^2+2y^2z^2+2z^2x^2-x^4-y^4-z^4}}, }$
καὶ
$\displaystyle{ x=d_2+d_3-d_1, \quad y=d_3+d_1-d_2, \quad z=d_1+d_2-d_3. }$

Ἀναμένω ἀπόδειξη!

Γ.-Σ. Σμυρλής · #5

Ἐπεκτείνομε τρεῖς ἀπὸ τὶς ἕξη πλευρὲς τοῦ ἑξαγώνου μήκους

(πρώτη, τρίτη καὶ πέμπτη), ὥστε νὰ σχηματισθεῖ τρίγωνο ABC

, ὅπως φαίνεται στὸ σχῆμα. Θέτομε a := |BC|

,

καὶ

ἐμβαδὸν τοῦ ABC

. Τὰ τρίγωνα ABC

,

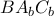καὶ

εἶναι ὅμοια καὶ συνεπῶς τὰ μήκη τῶν πλευρῶν τους εἶναι τὰ ἀναγραφόμενα στὸ σχῆμα. Γιὰ παράδειγμα BA_b=sc/b.

Ἄν

εἶναι τὸ ὕψος τοῦ τριγώνου ABC

ἀπὸ τὸ

, τότε ἔχομε
$\displaystyle{ \frac{|BB_c|}{|BC|} = \frac{k}{|H_C|} \quad\longrightarrow\quad \frac{s(a+b)}{ab} = \frac{k}{2T/c} \quad\longrightarrow\quad a b ck=2Ts(a+b). }$
Παρομοίως
$a b c h = 2 T s (b+c),\, a b c j = 2 T s (c+a) ,$
καὶ ὡς ἐκ τούτου
$\displaystyle{ \frac{h}{b+c}=\frac{j}{c+a}=\frac{k}{a+b}=\lambda, }$
γιὰ κάποιο
$\lambda>0$ .
Ἐπίσης
$\displaystyle{ abc(h+j+k)=4Ts(a+b+c). }$
Συνεπῶς
$\displaystyle{ a = (-h + j + k)\lambda, \qquad b = (h-j+k)\lambda, \qquad c = (h+j-k)\lambda, }$
καὶ
$\displaystyle{ T=\frac{abc(h+j+k)}{4s(a+b+c)}=\frac{\lambda^2(-h+j+k)(h-j+k)(h+j-k)}{4s}.\eqno{(1)} }$
Χάριν τοῦ τύπου τοῦ Ἥρωνος
$\displaystyle{ T =\frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)} }$
$\displaystyle{ = \frac{\lambda^2}{4}\sqrt{(h+j+k)(3h-j-k)(3j-k-h)(3k-h-j)}. }$
Τελικῶς, συνδυάζοντας τὴν ἀνωτέρω μὲ τὴν
(1)

,
λαμβάνομε
$\displaystyle{ s =\frac{(-h+j+k)(h-j+k)(h+j-k)}{\sqrt{(h+j+k)(3h-j-k)(3j-k-h)(3k-h-j)}} }$
Τὸ ἐμβαδὸν τοῦ ἑξαγώνου ἰσοῦται λοιπὸν μὲ
$\displaystyle{ E=\frac{s}{2}(h+j+k)=\frac{(h+j+k)(-h+j+k)(h-j+k)(h+j-k)}{2\sqrt{(h+j+k)(3h-j-k)(3j-k-h)(3k-h-j)}} . }$

Ὑπολογισμὸς ἐμβαδοῦ ἐξαγώνου

Ὑπολογισμὸς ἐμβαδοῦ ἐξαγώνου

Re: Ὑπολογισμὸς ἐμβαδοῦ ἐξαγώνου

Re: Ὑπολογισμὸς ἐμβαδοῦ ἐξαγώνου

Re: Ὑπολογισμὸς ἐμβαδοῦ ἐξαγώνου

Re: Ὑπολογισμὸς ἐμβαδοῦ ἐξαγώνου

Μέλη σε σύνδεση