 είναι εγγεγραμμένο σε κύκλο
είναι εγγεγραμμένο σε κύκλο  ,
, του οποίου τα σημεία του
 , είναι τα αντιδιαμετρικά των
, είναι τα αντιδιαμετρικά των  αντίστοιχα .
αντίστοιχα .Οι τομές των ευθειών
 σχηματίζουν το τρίγωνο
σχηματίζουν το τρίγωνο 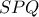 .
.α) Δείξτε ότι το
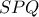 είναι όμοιο προς το
είναι όμοιο προς το 
β) Για ποια "μορφή" του
 , είναι
, είναι 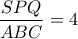 ;
;γ) Υπολογίστε την ελάχιστη τιμή του λόγου


 .
. , οπότε τα τρίγωνα
, οπότε τα τρίγωνα  είναι όμοια.
είναι όμοια. (1).
(1). (2).
(2). (3).
(3). (4).
(4). (5).
(5). (6).
(6).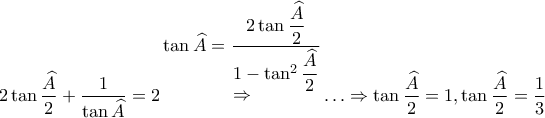
 , άτοπο, αφού
, άτοπο, αφού  .
.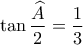 . Έστω
. Έστω  το ύψος του
το ύψος του  .
. .
. .
. και αντικαθιστώντας
και αντικαθιστώντας 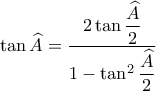 θα προκύψει
θα προκύψει  .
. με το ίσον για
με το ίσον για  , όταν δηλαδή
, όταν δηλαδή