 ειναι εγγεγραμμένο σε κύκλο και έστω
ειναι εγγεγραμμένο σε κύκλο και έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  .
.Αν
 σημεία των
σημεία των  αντίστοιχα, τέτοια ώστε
αντίστοιχα, τέτοια ώστε  και οι
και οι  τέμνουν την
τέμνουν την  στα
στα  αντίστοιχα,
αντίστοιχα, δείξτε ότι :

Αφιερωμένο στην ομάδα που μας έκανε περήφανους με την επιτυχία της στην ΙΜΟ2017
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 ειναι εγγεγραμμένο σε κύκλο και έστω
ειναι εγγεγραμμένο σε κύκλο και έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  .
. σημεία των
σημεία των  αντίστοιχα, τέτοια ώστε
αντίστοιχα, τέτοια ώστε  και οι
και οι  τέμνουν την
τέμνουν την  στα
στα  αντίστοιχα,
αντίστοιχα, 
Καλησπέρα.sakis1963 έγραψε: Ισοσκελές τρίγωνοειναι εγγεγραμμένο σε κύκλο και έστω
το αντιδιαμετρικό του
.
Ανσημεία των
αντίστοιχα, τέτοια ώστε
και οι
τέμνουν την
στα
αντίστοιχα,
δείξτε ότι :
Αφιερωμένο στην ομάδα που μας έκανε περήφανους με την επιτυχία της στην ΙΜΟ2017





 είναι το παράκεντρο ενός τριγώνου
είναι το παράκεντρο ενός τριγώνου  το οποίο αντιστοιχεί στην πλευρά
το οποίο αντιστοιχεί στην πλευρά 
 είναι το σημείο τομής των τμημάτων
είναι το σημείο τομής των τμημάτων  ,
,  είναι τα σημεία τομής των τμημάτων
είναι τα σημεία τομής των τμημάτων  με το τμήμα
με το τμήμα  , όπου
, όπου 
 με τις ημιευθείες
με τις ημιευθείες  του τριγώνου. (Σχ.2)
Απόδειξη:
του τριγώνου. (Σχ.2)
Απόδειξη: το σημείο τομής της
το σημείο τομής της  με την
με την 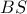 , όπου:
, όπου: .
.  είναι κάθετη στην
είναι κάθετη στην  Φέρουμε ακόμα τα τμήματα
Φέρουμε ακόμα τα τμήματα  και
και  τα οποία θα δείξουμε ότι είναι συνευθειακά.
τα οποία θα δείξουμε ότι είναι συνευθειακά.  προκύπτει:
προκύπτει: 
 προκύπτει:
προκύπτει:
 προκύπτει:
προκύπτει: 

 είναι συνευθειακά και συνεπώς το σημείο
είναι συνευθειακά και συνεπώς το σημείο 
 με την
με την  .
.  με το σημείο
με το σημείο  ως η τομή της
ως η τομή της  με την
με την  είναι κάθετη στην
είναι κάθετη στην 
 .
. 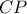 είναι κάθετο στην
είναι κάθετο στην  , δηλαδή το δεύτερο ύψος του τριγώνου
, δηλαδή το δεύτερο ύψος του τριγώνου  .
.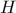 του τριγώνου αυτού από το οποίο θα διέλθει και το τρίτο ύψος
του τριγώνου αυτού από το οποίο θα διέλθει και το τρίτο ύψος  .
. την παράλληλη
την παράλληλη  προς την πλευρά
προς την πλευρά 
 στο σημείο
στο σημείο  . Θα δείξουμε ότι το σημείο αυτό
. Θα δείξουμε ότι το σημείο αυτό  είναι το μέσον της
είναι το μέσον της  . (Πρόταση 2)
. (Πρόταση 2) εύκολα διαπιστώνεται ότι
εύκολα διαπιστώνεται ότι 
 είναι διχοτόμος της εξωτερικής γωνίας
είναι διχοτόμος της εξωτερικής γωνίας  , θα είναι:
, θα είναι:

 είναι ισοσκελές καθόσον το τρίγωνο
είναι ισοσκελές καθόσον το τρίγωνο  είναι ορθογώνιο.
είναι ορθογώνιο. είναι μέσον της
είναι μέσον της  .
. προς την πλευρά
προς την πλευρά  διέρχεται κι αυτή από το μέσον
διέρχεται κι αυτή από το μέσον  της πλευράς
της πλευράς  .
. και
και 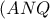
 παράλληλα προς τις αντίστοιχες βάσεις των επί των παραλλήλων
παράλληλα προς τις αντίστοιχες βάσεις των επί των παραλλήλων  .
. Στην προέκταση τηςsakis1963 έγραψε:GEOMETRIA187=FB994.png
Ισοσκελές τρίγωνοειναι εγγεγραμμένο σε κύκλο και έστω
το αντιδιαμετρικό του
.
Ανσημεία των
αντίστοιχα, τέτοια ώστε
και οι
τέμνουν την
στα
αντίστοιχα,
δείξτε ότι :
Αφιερωμένο στην ομάδα που μας έκανε περήφανους με την επιτυχία της στην ΙΜΟ2017
 θεωρούμε σημείο
θεωρούμε σημείο  με
με  οπότε
οπότε 
 είναι ίσα αφού
είναι ίσα αφού  ,άρα
,άρα  και
και 
 και
και  και
και 
 εγγράψιμο ,συνεπώς
εγγράψιμο ,συνεπώς 
 εγγράψιμο
εγγράψιμο εγγράψιμο
εγγράψιμο
 ως συμπληρώματα των ίσων γωνιών
ως συμπληρώματα των ίσων γωνιών  και
και  ως συμπληρώματα των ίσων γωνιών
ως συμπληρώματα των ίσων γωνιών 
 .Ακόμη,
.Ακόμη, 

 .Ακόμη,
.Ακόμη, 

 έχουμε
έχουμε ή
ή

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες