Διονύσιος Αδαμόπουλος έγραψε:...Το θεώρημα ανάλογων διαιρέσεων μπορούμε να το χρησιμοποιήσουμε χωρίς απόδειξη σε διαγωνισμό προχωρημένης φάσης; Είναι γενικά γνωστό;

Αυτό το απλό στην διατύπωσή του και πολύ εύκολο στην απόδειξή του θεώρημα ( άμεση εφαρμογή του
Θεωρήματος Θαλή ), δεν είναι ευρέως γνωστό στην ελληνική βιβλιογραφία ( την παλιότερη, μέχρι το 2000 ), που έχω υπόψη μου. Προσωπικά, το θεωρούσα δική μου κατασκευή, μέχρι που το ανακάλυψα ( πριν μία πενταετία περίπου ) σε ένα βιβλίο του Ι. ΙΩΑΝΝΙΔΗ, σχετικό με γεωμετρικούς τόπους. (*)
Τα τελευταία χρόνια εμφανίστηκε ( το θεώρημα ) στο διαδίκτυο και βασισμένες σ' αυτό, δόθηκαν αρκετές αποδείξεις, ενίοτε δύσκολων προβλημάτων.
Δηλώνω αναρμόδιος να απαντήσω στο ερώτημα εάν μπορεί να χρησιμοποιηθεί το θεώρημα αυτό χωρίς απόδειξη, αφού στο μόνο σύγχρονο βιβλίο που έχω δει αναφορά του, είναι σε βιβλίο του Σιλουανού (**), όπου μάλιστα η απόδειξή του παραλείπεται, ως πολύ απλή. Ο Σιλουανός ( το ίδιο ίσως και κάποιοι άλλοι ) σίγουρα, εκτιμώ, θα το δεχόταν χωρίς απόδειξη.
Νομίζω όμως, ότι εν γένει δεν είναι αποδεκτό χωρίς απόδειξη. Ας απαντήσουν άλλοι πιο αρμόδιοι.
(*) Ι. ΙΩΑΝΝΙΔΗΣ - ΓΕΩΜΕΤΡΙΑ II - Γεωμετρικοί τόποι - Σελίδα 181 - Αυτοέκδοση (;) - Αθήνα 1964
(**) ΧΑΡΑΛΑΜΠΟΣ ΣΤΕΡΓΙΟΥ, ΣΙΛΟΥΑΝΟΣ ΜΠΡΑΖΙΤΙΚΟΣ - Μαθηματικοί Διαγωνισμοί 2 - Σελίδα 215 - Εκδόσεις Σαββάλας - Αθήνα 2013
Κώστας Βήττας.
 ισόπλευρο τρίγωνο. Από τα
ισόπλευρο τρίγωνο. Από τα  και
και  φέρνουμε κάθετες στις
φέρνουμε κάθετες στις  και
και  αντίστοιχα που τέμνονται στο
αντίστοιχα που τέμνονται στο  . Έστω
. Έστω  τυχαίο σημείο της
τυχαίο σημείο της  . Φέρνουμε από το
. Φέρνουμε από το  κάθετες στις
κάθετες στις  και
και  , οι οποίες τέμνουν τις
, οι οποίες τέμνουν τις  και
και  στα
στα  και
και  αντίστοιχα. Έστω
αντίστοιχα. Έστω  το μέσο του
το μέσο του  . Να αποδειχθεί πως τα σημεία
. Να αποδειχθεί πως τα σημεία 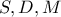 είναι συνευθειακά.
είναι συνευθειακά.
 Έστω τα σημεία
Έστω τα σημεία  και
και  και ας είναι
και ας είναι  , οι προβολές του σημείου
, οι προβολές του σημείου  , αντιστοίχως.
, αντιστοίχως. λόγω
λόγω 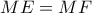 και
και  και ομοίως έχουμε
και ομοίως έχουμε  λόγω
λόγω  .
. και
και  όπου
όπου  και
και  .
. και
και 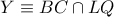 .
.
 , ισχύει
, ισχύει  λόγω
λόγω  και ομοίως έχουμε
και ομοίως έχουμε 
 τώρα, είναι ισόπλευρο λόγω της
τώρα, είναι ισόπλευρο λόγω της  και
και  από το εγγράψιμο τετράπλευρο
από το εγγράψιμο τετράπλευρο 
 λόγω
λόγω  .
. γιατί
γιατί  , στο ισόπλευρο τρίγωνο
, στο ισόπλευρο τρίγωνο  , λόγω της
, λόγω της  και
και  .
.  , έχουμε
, έχουμε  και από τα όμοια ορθογώνια τρίγωνα
και από τα όμοια ορθογώνια τρίγωνα  , έχουμε
, έχουμε  γιατί ισχύει
γιατί ισχύει  και
και  .
.

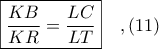
 , σύμφωνα με το
, σύμφωνα με το  είναι συνευθειακά και το ζητούμενο έχει αποδειχθεί.
είναι συνευθειακά και το ζητούμενο έχει αποδειχθεί. , οι
, οι  είναι ομόλογες ευθείες και επομένως αληθεύει η
είναι ομόλογες ευθείες και επομένως αληθεύει η  ,αρκεί
,αρκεί  (η
(η  διχοτομεί την
διχοτομεί την  ).Όμως,
).Όμως, ,με K,L ορισμένα όπως παραπάνω.Το ζητούμενο έπεται από θ. Διχοτόμων-ομοιότητα στα
,με K,L ορισμένα όπως παραπάνω.Το ζητούμενο έπεται από θ. Διχοτόμων-ομοιότητα στα  ..
..