 έχει
έχει  . Η
. Η  είναι διχοτόμος ,
είναι διχοτόμος ,το
 η προβολή του
η προβολή του  στην
στην  και το
και το  η προβολή του
η προβολή του  στην
στην  .
.Αν το
 είναι συγχρόνως και μέσο της
είναι συγχρόνως και μέσο της  , υπολογίστε το μήκος της
, υπολογίστε το μήκος της  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 έχει
έχει  . Η
. Η  είναι διχοτόμος ,
είναι διχοτόμος , η προβολή του
η προβολή του  στην
στην  και το
και το  η προβολή του
η προβολή του  στην
στην  .
. είναι συγχρόνως και μέσο της
είναι συγχρόνως και μέσο της  , υπολογίστε το μήκος της
, υπολογίστε το μήκος της  .
.
 θα τμήση την ευθεία
θα τμήση την ευθεία  στα αντιδιαμετρικά σημεία
στα αντιδιαμετρικά σημεία  ( το
( το  ανάμεσα στα
ανάμεσα στα  ) και έστω
) και έστω  το αντιδιαμέτρικό του
το αντιδιαμέτρικό του  σ αυτό τον κύκλο .
σ αυτό τον κύκλο . το
το  είναι βαρύκεντρο και άρα
είναι βαρύκεντρο και άρα  . Επειδή
. Επειδή  προκύπτει
προκύπτει 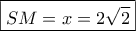
 τέμνει το άνω ημικύκλιο του
τέμνει το άνω ημικύκλιο του  στο
στο  το οποίο αποτελεί λύση του προβλήματος
το οποίο αποτελεί λύση του προβλήματος στην προέκτασή της τέμνει το ημικύκλιο στο
στην προέκτασή της τέμνει το ημικύκλιο στο 
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 7 επισκέπτες