 του τετραγώνου
του τετραγώνου  , θεωρούμε σημεία
, θεωρούμε σημεία 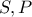 αντίστοιχα ,
αντίστοιχα , ώστε :
 . Ο κύκλος διαμέτρου
. Ο κύκλος διαμέτρου  , τέμνει τη διαγώνιο
, τέμνει τη διαγώνιο 
στα σημεία
 . Δείξτε ότι οι οι προεκτάσεις των
. Δείξτε ότι οι οι προεκτάσεις των  , διέρχονται από το
, διέρχονται από το  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 του τετραγώνου
του τετραγώνου  , θεωρούμε σημεία
, θεωρούμε σημεία 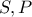 αντίστοιχα ,
αντίστοιχα ,  . Ο κύκλος διαμέτρου
. Ο κύκλος διαμέτρου  , τέμνει τη διαγώνιο
, τέμνει τη διαγώνιο 
 . Δείξτε ότι οι οι προεκτάσεις των
. Δείξτε ότι οι οι προεκτάσεις των  , διέρχονται από το
, διέρχονται από το  .
. διχοτομεί τις ορθές γωνίες στα
διχοτομεί τις ορθές γωνίες στα  , θα δείξω
, θα δείξω  τμήσουν τη διαγώνιο στα
τμήσουν τη διαγώνιο στα  τότε τα
σημεία
τότε τα
σημεία  ανήκουν σε ένα κύκλο.
ανήκουν σε ένα κύκλο. και αφού
και αφού  . Άμεση συνέπεια : το τετράπλευρο
. Άμεση συνέπεια : το τετράπλευρο  είναι εγγράψιμο , Έτσι
είναι εγγράψιμο , Έτσι  .Ομοίως και
.Ομοίως και  ..
.. είναι εγγράψιμα .
είναι εγγράψιμα . ανήκουν σε ένα κύκλο..
ανήκουν σε ένα κύκλο.. .
.  του τραπεζίου
του τραπεζίου  και κόψει την
και κόψει την  στο
στο  θα έχω :
θα έχω : συνεπώς ,
συνεπώς ,  .
. έχω ότι , αν
έχω ότι , αν  τότε
τότε  .
. αληθές λόγω Π. Θ. στο
αληθές λόγω Π. Θ. στο  , το τετράπλευρο
, το τετράπλευρο  είναι εγγράψιμο και άρα
είναι εγγράψιμο και άρα  .
."Πειράζω" λίγο την εκφώνηση. Θεωρώ
 τα σημεία στα οποία οι
τα σημεία στα οποία οι  τέμνουν τον κύκλο και θα δείξω
τέμνουν τον κύκλο και θα δείξω  Με Πυθαγόρειο βρίσκω
Με Πυθαγόρειο βρίσκω  και με νόμο συνημιτόνων στο
και με νόμο συνημιτόνων στο  διαπιστώνω
διαπιστώνω  Αλλά το
Αλλά το  είναι εγγράψιμο, οπότε
είναι εγγράψιμο, οπότε  Επειδή όμως είναι και
Επειδή όμως είναι και 
 θα είναι συνευθειακά, ομοίως και το
θα είναι συνευθειακά, ομοίως και το 
Στο σχήμα του Θανάση.
 τα σημεία που τέμνουν οι
τα σημεία που τέμνουν οι  την διαγώνιο.
την διαγώνιο. βρίσκονται πάνω σε κύκλο διαμέτρου
βρίσκονται πάνω σε κύκλο διαμέτρου  .
. το μέσο της
το μέσο της  .
. καθετος στην
καθετος στην 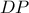 .
.
 παράλληλη
παράλληλη  και τελειώσαμε για το
και τελειώσαμε για το  .
.
 βρίσκεται πάνω στον κύκλο.
βρίσκεται πάνω στον κύκλο. τέμνονται στο σημείο
τέμνονται στο σημείο 






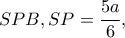



 Έστω το σημείο
Έστω το σημείο  και έχουμε
και έχουμε 
 κάθετη ευθεία επί τη
κάθετη ευθεία επί τη  τέμνει την
τέμνει την  στο σημείο έστω
στο σημείο έστω  και από το ορθογώνιο τρίγωνο
και από το ορθογώνιο τρίγωνο  με
με 

 λόγω
λόγω  και
και  .
.



 λόγω
λόγω  και
και  Από
Από 

 λόγω
λόγω  .
. προκύπτει ότι το σημείο
προκύπτει ότι το σημείο  ανήκει στον περίκυκλο έστω
ανήκει στον περίκυκλο έστω  του ορθογωνίου τριγώνου
του ορθογωνίου τριγώνου  λόγω της διαμέτρου
λόγω της διαμέτρου  .
. Η δια του σημείου
Η δια του σημείου  παράλληλη ευθεία προς την
παράλληλη ευθεία προς την  , περνάει από το μέσον του
, περνάει από το μέσον του  λόγω της
λόγω της  και προφανώς, από το μέσον
και προφανώς, από το μέσον  του
του  .
. παράλληλη ευθεία προς την
παράλληλη ευθεία προς την  , περνάει από το μέσον του
, περνάει από το μέσον του  και προφανώς από το μέσον
και προφανώς από το μέσον  του
του  ,
,  από
από  .
. τώρα, είναι ορθογώνιο ισοσκελές ( προφανές ) και άρα, έχουμε
τώρα, είναι ορθογώνιο ισοσκελές ( προφανές ) και άρα, έχουμε 
 συμπεραίνεται ότι το σημείο
συμπεραίνεται ότι το σημείο  ανήκει επίσης στον κύκλο
ανήκει επίσης στον κύκλο  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.
 έχουμε
έχουμε  και
και 
 του τραπεζίου
του τραπεζίου  είναι
είναι  και με Π.Θ
και με Π.Θ  και
και 
 .Έτσι,λόγω προφανούς ισότητας των
.Έτσι,λόγω προφανούς ισότητας των και του εγγράψιμου
και του εγγράψιμου  συνευθειακά
συνευθειακά και
και  , είναι
, είναι 
 είναι συνευθειακά
είναι συνευθειακάΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες