 , θεωρούμε σημεία
, θεωρούμε σημεία 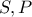 , ώστε :
, ώστε :  και
και  . Η διχοτόμος της
. Η διχοτόμος της  , τέμνει
, τέμνει την
 στο σημείο
στο σημείο  . Αν
. Αν  , υπολογίστε την
, υπολογίστε την  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , θεωρούμε σημεία
, θεωρούμε σημεία 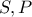 , ώστε :
, ώστε :  και
και  . Η διχοτόμος της
. Η διχοτόμος της  , τέμνει
, τέμνει  στο σημείο
στο σημείο  . Αν
. Αν  , υπολογίστε την
, υπολογίστε την  .
. ισόπλευρο, άρα
ισόπλευρο, άρα  Επομένως έχω
Επομένως έχω  και άρα
και άρα  Συνεπώς έχω
Συνεπώς έχω  Από θεώρημα διχοτόμου στο
Από θεώρημα διχοτόμου στο  έχω
έχω 

Η καθεμία από τις πράσινες γωνίες είναι
 και η
και η  εφάπτεται στον περίκυκλο του
εφάπτεται στον περίκυκλο του 

 Είναι ακόμα
Είναι ακόμα  Με νόμο ημιτόνων στα τρίγωνα
Με νόμο ημιτόνων στα τρίγωνα  έχω:
έχω:

 και
και 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες