 του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  , θεωρούμε σημείο
, θεωρούμε σημείο  .
.Η προέκταση του ύψους
 τέμνει το
τέμνει το  στο
στο  , από το οποίο φέρουμε
, από το οποίο φέρουμε 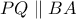 .
.α) Δείξτε ότι η ευθεία
 διέρχεται από του μέσο
διέρχεται από του μέσο  του
του  .
.β) Δείξτε ότι το τετράπλευρο
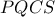 δεν είναι εγγράψιμο .
δεν είναι εγγράψιμο .γ) Δείξτε ότι :


Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 του ισοσκελούς τριγώνου
του ισοσκελούς τριγώνου  , θεωρούμε σημείο
, θεωρούμε σημείο  .
. τέμνει το
τέμνει το  στο
στο  , από το οποίο φέρουμε
, από το οποίο φέρουμε 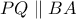 .
. διέρχεται από του μέσο
διέρχεται από του μέσο  του
του  .
.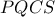 δεν είναι εγγράψιμο .
δεν είναι εγγράψιμο .

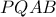 η
η  διέρχεται από το μέσο
διέρχεται από το μέσο  της βάσης
της βάσης  .
.  είναι διάμεσος προς την υποτείνουσα του ορθογωνίου τριγώνου
είναι διάμεσος προς την υποτείνουσα του ορθογωνίου τριγώνου  .
. οπότε το
οπότε το  μέσο της
μέσο της  .
.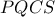 ήταν εγγράψιμο θα ήταν και
ήταν εγγράψιμο θα ήταν και  ( άτοπο ).
( άτοπο ). με διατέμνουσα
με διατέμνουσα  και Θ. διχοτόμου έχω :
και Θ. διχοτόμου έχω : άρα :
άρα :  .
.KARKAR έγραψε: ↑Παρ Μαρ 16, 2018 7:40 pmΠεριπέτεια με προέκταση.pngΣτην προέκταση της πλευράςτου ισοσκελούς τριγώνου
, θεωρούμε σημείο
.
Η προέκταση του ύψουςτέμνει το
στο
, από το οποίο φέρουμε
.
α) Δείξτε ότι η ευθείαδιέρχεται από του μέσο
του
.
β) Δείξτε ότι το τετράπλευροδεν είναι εγγράψιμο .
γ) Δείξτε ότι :

 και Ceva στο
και Ceva στο 
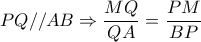 άρα
άρα  .Άρα
.Άρα  μέσον της
μέσον της 
 οι πράσινες γωνίες θα ήταν ίσες που είναι άτοπο αφού
οι πράσινες γωνίες θα ήταν ίσες που είναι άτοπο αφού 
 διχοτόμος της
διχοτόμος της  και
και 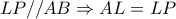 .Επιπλέον, οι γωνίες
.Επιπλέον, οι γωνίες  του σχήματος
του σχήματος
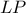 είναι εφαπτόμενη του περίκυκλου του
είναι εφαπτόμενη του περίκυκλου του  οπότε
οπότε 
 και
και  κι επομένως
κι επομένως 
KARKAR έγραψε: ↑Παρ Μαρ 16, 2018 7:40 pmΠεριπέτεια με προέκταση.pngΣτην προέκταση της πλευράςτου ισοσκελούς τριγώνου
, θεωρούμε σημείο
.
Η προέκταση του ύψουςτέμνει το
στο
, από το οποίο φέρουμε
.
α) Δείξτε ότι η ευθείαδιέρχεται από του μέσο
του
.
β) Δείξτε ότι το τετράπλευροδεν είναι εγγράψιμο .
γ) Δείξτε ότι :




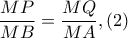





 με τέμνουσα
με τέμνουσα 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες