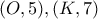 εφάπτονται εξωτερικά στο
εφάπτονται εξωτερικά στο  και έστω
και έστω  ο βόρειος και
ο βόρειος και  ο νότιος πόλος του κύκλου
ο νότιος πόλος του κύκλου 
Οι
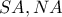 τέμνουν τον κύκλο
τέμνουν τον κύκλο  στα
στα 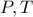 αντίστοιχα. Επιλέγουμε το σημείο
αντίστοιχα. Επιλέγουμε το σημείο  του κύκλου
του κύκλου  ώστε
ώστε 
και το σημείο
 του ίδιου κύκλου, ώστε το εμβαδόν του τριγώνου
του ίδιου κύκλου, ώστε το εμβαδόν του τριγώνου 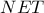 να είναι το μέγιστο δυνατόν. Να βρείτε το λόγο
να είναι το μέγιστο δυνατόν. Να βρείτε το λόγο και να δικαιολογήσετε τον τίτλο.
και να δικαιολογήσετε τον τίτλο.
 το μέσον του
το μέσον του  ,
, 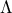 η προβολή του
η προβολή του  στην
στην  και
και 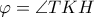 .
.  και
και 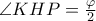 .
.  γίνεται μέγιστο όταν το
γίνεται μέγιστο όταν το 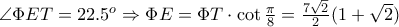 και
και 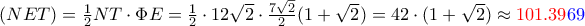 .
.  και
και 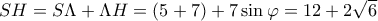 οπότε
οπότε 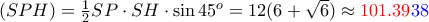 .
. 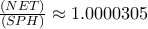 , οπότε πράγματι τα
, οπότε πράγματι τα 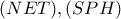 είναι... παρά τρίχα ίσα!
είναι... παρά τρίχα ίσα!