 , του ορθογωνίου τριγώνου
, του ορθογωνίου τριγώνου  , θεωρούμε
, θεωρούμε σημεία :
 αντίστοιχα , ώστε :
αντίστοιχα , ώστε :  και ονομάζω
και ονομάζω  τις προβολές τους στην
τις προβολές τους στην υποτείνουσα
 . Βρείτε το μέγιστο εμβαδόν του ορθογωνίου τραπεζίου
. Βρείτε το μέγιστο εμβαδόν του ορθογωνίου τραπεζίου  .
. , του ορθογωνίου τριγώνου
, του ορθογωνίου τριγώνου  , θεωρούμε
, θεωρούμε  αντίστοιχα , ώστε :
αντίστοιχα , ώστε :  και ονομάζω
και ονομάζω  τις προβολές τους στην
τις προβολές τους στην  . Βρείτε το μέγιστο εμβαδόν του ορθογωνίου τραπεζίου
. Βρείτε το μέγιστο εμβαδόν του ορθογωνίου τραπεζίου  .
.Καλησπέρα και Χρόνια Πολλά...


 είναι:
είναι: 



 με
με  .
. .
.  στην
στην  έχει εξίσωση
έχει εξίσωση 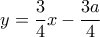 και την τέμνει στο
και την τέμνει στο  .
. στην
στην  έχει εξίσωση
έχει εξίσωση  και την τέμνει στο
και την τέμνει στο  .
.
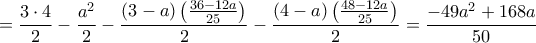 .
. έχει μέγιστο για
έχει μέγιστο για  ,
, 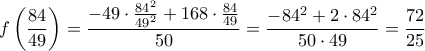 .
. ) τρίγωνο
) τρίγωνο  .
. έχω
έχω  ( κάποιο πρόβλημα στο
( κάποιο πρόβλημα στο  )
) , τη διχοτόμο
, τη διχοτόμο  και
και  θεωρώ δε, χωρίς βλάβη της γενικότητας
θεωρώ δε, χωρίς βλάβη της γενικότητας  .
. . Φέρνω δηλαδή
. Φέρνω δηλαδή  .
. , όμως θα δείξω ότι πάντα
, όμως θα δείξω ότι πάντα 
 ) και άρα έχω μεγιστοποίηση όταν
) και άρα έχω μεγιστοποίηση όταν  (2)
(2)
 είναι όμοια θα έχω :
είναι όμοια θα έχω : ,
,  Γιατί
Γιατί  .
. 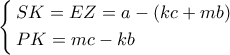 κι έτσι η
κι έτσι η  δίδει.
δίδει.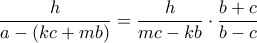 και άρα
και άρα 
 και δεδομένου ότι
και δεδομένου ότι  , δίδει :
, δίδει :  . Πολλαπλασιάζω με
. Πολλαπλασιάζω με  και προκύπτει :
και προκύπτει :  . Τώρα η
. Τώρα η  δίδει :
δίδει : .
. .
. 
 .
. και ομοίως :
και ομοίως : 
 και ομοίως :
και ομοίως :  . Επομένως :
. Επομένως :  .
. , το οποίο είναι το :
, το οποίο είναι το :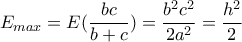 , αφού (
, αφού (  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες