 , στο οποίο η γωνία που σχηματίζουν
, στο οποίο η γωνία που σχηματίζουνη διάμεσος
 με την διχοτόμο
με την διχοτόμο  , να ισούται με το μισό της γωνίας
, να ισούται με το μισό της γωνίας 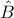 .
. , στο οποίο η γωνία που σχηματίζουν
, στο οποίο η γωνία που σχηματίζουν με την διχοτόμο
με την διχοτόμο  , να ισούται με το μισό της γωνίας
, να ισούται με το μισό της γωνίας 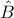 .
.Κατασκευάζω το ορθογώνιο τρίγωνο
 με πλευρές
με πλευρές  .
Απόδειξη: Φέρνω και τη διχοτόμο
.
Απόδειξη: Φέρνω και τη διχοτόμο  Είναι
Είναι 

 Άρα,
Άρα,  και ολοκληρώνεται η απόδειξη.
και ολοκληρώνεται η απόδειξη. .
. .
. είναι ορθογώνιο και ισοσκελές. Η συνέχεια της κατασκευής είναι απλή.
είναι ορθογώνιο και ισοσκελές. Η συνέχεια της κατασκευής είναι απλή.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες