 ;
;Euler 2013/3
Συντονιστές: achilleas, emouroukos, silouan
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Euler 2013/3
Ορίζουμε την ακολουθία  με
με  . Παρατηρούμε ότι
. Παρατηρούμε ότι 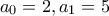 .
.
Επίσης, .
.
Έτσι, τα υπόλοιπα με το των πρώτων όρων της
των πρώτων όρων της  είναι
είναι  και επαναλαμβάνονται με περίοδο
και επαναλαμβάνονται με περίοδο  . Αφού
. Αφού  , ισχύει
, ισχύει  και το τελευταίο ψηφίο του
και το τελευταίο ψηφίο του 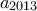 είναι
είναι  .
.
Λαμβάνοντας υπόψιν ότι , καταλήγουμε στο συμπέρασμα ότι το τελευταίο ψηφίο του
, καταλήγουμε στο συμπέρασμα ότι το τελευταίο ψηφίο του  είναι
είναι  .
.
 με
με  . Παρατηρούμε ότι
. Παρατηρούμε ότι 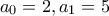 .
. Επίσης,
 .
.Έτσι, τα υπόλοιπα με το
 των πρώτων όρων της
των πρώτων όρων της  είναι
είναι  και επαναλαμβάνονται με περίοδο
και επαναλαμβάνονται με περίοδο  . Αφού
. Αφού  , ισχύει
, ισχύει  και το τελευταίο ψηφίο του
και το τελευταίο ψηφίο του 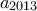 είναι
είναι  .
. Λαμβάνοντας υπόψιν ότι
 , καταλήγουμε στο συμπέρασμα ότι το τελευταίο ψηφίο του
, καταλήγουμε στο συμπέρασμα ότι το τελευταίο ψηφίο του  είναι
είναι  .
.Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Euler 2013/3
Σωστά!
Να υπενθυμίσουμε ότι οι ακολουθίες της μορφής έχουν λύσεις της μορφής
έχουν λύσεις της μορφής 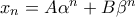 όπου τα
όπου τα  είναι ρίζες της
είναι ρίζες της  και τα
και τα  καθορίζονται από τις αρχικές τιμές.
καθορίζονται από τις αρχικές τιμές.
Ισχύει και το αντίστροφο. Εδώ οι ρίζες είναι οι με άθροισμα
με άθροισμα  και γινόμενο
και γινόμενο  οπότε η ακολουθία ικανοποιεί την αναδρομική σχέση
οπότε η ακολουθία ικανοποιεί την αναδρομική σχέση 
Να υπενθυμίσουμε ότι οι ακολουθίες της μορφής
 έχουν λύσεις της μορφής
έχουν λύσεις της μορφής 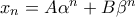 όπου τα
όπου τα  είναι ρίζες της
είναι ρίζες της  και τα
και τα  καθορίζονται από τις αρχικές τιμές.
καθορίζονται από τις αρχικές τιμές.Ισχύει και το αντίστροφο. Εδώ οι ρίζες είναι οι
 με άθροισμα
με άθροισμα  και γινόμενο
και γινόμενο  οπότε η ακολουθία ικανοποιεί την αναδρομική σχέση
οπότε η ακολουθία ικανοποιεί την αναδρομική σχέση 
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
