 και
και 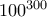
Πρόκειται για μία άσκηση που μου είχε κοινοποιήσει πριν από 6 περίπου χρόνια ο συνάδελφος Πρόδρομος Ελευθερίου από τη Μυτιλήνη και την οποία θυμήθηκα με αφορμή μία άλλη παρόμοια άσκηση.
Αλέξανδρος
Συντονιστές: achilleas, emouroukos, silouan
 και
και 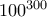




Καλώς ήλθες στο φόρουμ.perception έγραψε:Καλησπέρα σας,
μια λύση θα ήθελα να προτείνω(αν είναι σωστή φυσικά).
Ισχύει η ανισοτική σχέση
Συνεπώς:
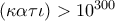 ενώ το ζητούμενο είναι πολύ μεγαλύτερο:
ενώ το ζητούμενο είναι πολύ μεγαλύτερο:
perception έγραψε:
Μάλιστα ισχύειMihalis_Lambrou έγραψε:
Πολλά δεν πάνε καλά με την παραπάνω απόδειξη. Για παράδειγμα δείχνει μία
 άρα αυτός ο τρόπος αποτυγχάνει για την απόδειξη της ζητούμενες.
άρα αυτός ο τρόπος αποτυγχάνει για την απόδειξη της ζητούμενες.
 ισχύει
ισχύει

 που ισχύει.
που ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες