

![\mathbb{R}\left [ x \right ] \mathbb{R}\left [ x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b270ca5573aa6fc0a7a0bad089f638c7.png) που είναι τέτοια, ώστε:
που είναι τέτοια, ώστε:  ,
,  .
.Συντονιστές: achilleas, emouroukos, silouan


![\mathbb{R}\left [ x \right ] \mathbb{R}\left [ x \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b270ca5573aa6fc0a7a0bad089f638c7.png) που είναι τέτοια, ώστε:
που είναι τέτοια, ώστε:  ,
,  .
.Αρχικά 2 προφανείς λύσεις είναι οιnikos_el έγραψε:Να προσδιοριστούν όλα τα πολυώνυμα

που είναι τέτοια, ώστε:
,
.
 και
και 
 μία ρίζα του
μία ρίζα του  τότε από τη δοθείσα σχέση βλέπουμε πως και
τότε από τη δοθείσα σχέση βλέπουμε πως και  είναι ρίζα του
είναι ρίζα του  .Άρα για να μην έχουμε άπειρες ρίζες θα πρέπει
.Άρα για να μην έχουμε άπειρες ρίζες θα πρέπει  .Όμως παρατηρούμε ακόμα πως και η
.Όμως παρατηρούμε ακόμα πως και η  είναι ρίζα του
είναι ρίζα του  .Άρα θα πρέπει να απορρίψουμε και τις περιπτώσεις
.Άρα θα πρέπει να απορρίψουμε και τις περιπτώσεις  και
και  γιατί οδηγούμαστε σε άπειρες ρίζες πάλι.
γιατί οδηγούμαστε σε άπειρες ρίζες πάλι. και άρα
και άρα  που όμως ικανοποιεί την αρχική σχέση μόνο αν
που όμως ικανοποιεί την αρχική σχέση μόνο αν  ή
ή  άρα η απάντηση είναι κάθε πολυώνυμο της μορφής
άρα η απάντηση είναι κάθε πολυώνυμο της μορφής  , όπου
, όπου  θετικός ακέραιος, ή
θετικός ακέραιος, ή  ή
ή  .
. .
. 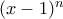 είναι μη μηδενικές λύσεις.
είναι μη μηδενικές λύσεις. και
και  Έστω
Έστω  ρίζα του πολυωνύμου.
ρίζα του πολυωνύμου.  . Επειδή το πολυώνυμο δε μπορεί να έχει άπειρες ρίζες, υπάρχουν φυσικοί
. Επειδή το πολυώνυμο δε μπορεί να έχει άπειρες ρίζες, υπάρχουν φυσικοί  ώστε
ώστε  (
( )
)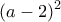 είναι ρίζα του πολυωνύμου, οπότε από την (
είναι ρίζα του πολυωνύμου, οπότε από την ( ) προκύπτει
) προκύπτει 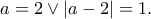
 Θέτοντας
Θέτοντας  βλέπουμε ότι
βλέπουμε ότι  δηλαδή
δηλαδή  Άρα
Άρα 
 άρα
άρα 
 είναι οι μόνες λύσεις.
είναι οι μόνες λύσεις.Επίσημα ναι. Από την σελίδα της Ε.Μ.Ε. "Εξεταστέα ύλη για τον τρίτο διαγωνισμό "ΑΡΧΙΜΗΔΗΣ" και τον «Προκριματικό διαγωνισμό» θεωρείται η ύλη των Διεθνών Μαθηματικών Ολυμπιάδων"dement έγραψε:
Περιέργεια (που φυσικά δεν ήθελα να εκφράσω πριν): Η ύλη του Αρχιμήδη περιλαμβάνει μιγαδικούς και Θεμελιώδες Θεώρημα Άλγεβρας;
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες