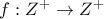 ,ώστε
,ώστε 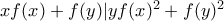 για κάθε ζεύγος θετικών ακεραίων
για κάθε ζεύγος θετικών ακεραίων  .
.Συντονιστές: achilleas, emouroukos, silouan
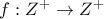 ,ώστε
,ώστε 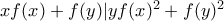 για κάθε ζεύγος θετικών ακεραίων
για κάθε ζεύγος θετικών ακεραίων  .
.Έχει λάθος
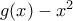 με g(x) τέτοιο ώστε να επαληθεύει τους περιοριμούς (θα το διώξουμε μετά όταν φτάσουμε στο σημείο που θα δούμε τη βολεύει). Οπότε
με g(x) τέτοιο ώστε να επαληθεύει τους περιοριμούς (θα το διώξουμε μετά όταν φτάσουμε στο σημείο που θα δούμε τη βολεύει). Οπότε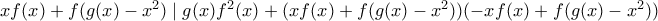
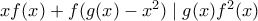

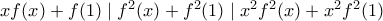 (b)
(b) το
το 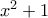 στην (α) (όταν έλυσα την άσκηση πρώτα έκανα αυτό και μετά το (b))
στην (α) (όταν έλυσα την άσκηση πρώτα έκανα αυτό και μετά το (b))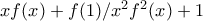 (c)
(c)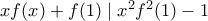 (d) Αυτό ισχύει για κάθε x θετικό ακέραιο
(d) Αυτό ισχύει για κάθε x θετικό ακέραιο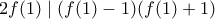 το οποίο ισχύει αν και μόνο αν
το οποίο ισχύει αν και μόνο αν  (απλή απόδειξη)
(απλή απόδειξη)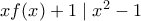 και τώρα όπου x το 3 έχουμε
και τώρα όπου x το 3 έχουμε 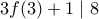 άτοπο αφού f(3) ακέραιος άρα δεν υπάρχει τέτοια συνάρτηση
άτοπο αφού f(3) ακέραιος άρα δεν υπάρχει τέτοια συνάρτηση άνω φραγμένη.Επειδή είναι κάτω φραγμένη,το
άνω φραγμένη.Επειδή είναι κάτω φραγμένη,το 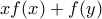 είναι μη φραγμένο για μεταβλητό
είναι μη φραγμένο για μεταβλητό  και
και  σταθερό,ενώ το
σταθερό,ενώ το 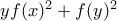 είναι φραγμένο-άτοπο.
είναι φραγμένο-άτοπο. μη φραγμένη.
μη φραγμένη.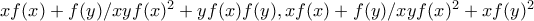 δηλαδή και
δηλαδή και 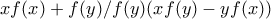 .
. .
. είναι μη φραγμένη,είναι απλό πως
είναι μη φραγμένη,είναι απλό πως 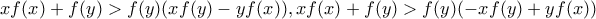 για μεγάλα
για μεγάλα  και συνεπώς η διαιρετότητα δεν μπορεί να ισχύει εκτός αν
και συνεπώς η διαιρετότητα δεν μπορεί να ισχύει εκτός αν 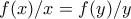 .Έτσι,για κάθε
.Έτσι,για κάθε  υπάρχει αρκετά μεγάλο
υπάρχει αρκετά μεγάλο  ώστε
ώστε 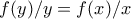 οπότε τελικά
οπότε τελικά 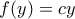
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες