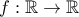 τέτοιες ώστε
τέτοιες ώστε 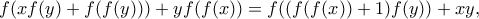 για κάθε
για κάθε 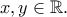
Συντονιστές: achilleas, emouroukos, silouan
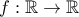 τέτοιες ώστε
τέτοιες ώστε 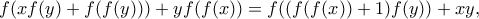 για κάθε
για κάθε 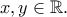
 για κάθε
για κάθε  ή
ή 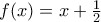 για κάθε
για κάθε  .
.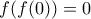 . Θα δείξω ότι
. Θα δείξω ότι  για κάθε
για κάθε 
 παίρνω
παίρνω 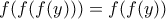 για κάθε
για κάθε  . Υποθέτω προς άτοπο ότι υπάρχει
. Υποθέτω προς άτοπο ότι υπάρχει  με
με 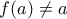 , έστω
, έστω 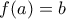 . Τότε
. Τότε 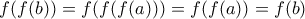 .
. 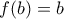 , τότε για
, τότε για 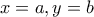 παίρνω
παίρνω 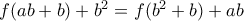 ενώ για
ενώ για 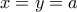 παίρνω
παίρνω 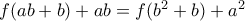 . Αφαιρώντας τις δύο σχέσεις παίρνω
. Αφαιρώντας τις δύο σχέσεις παίρνω 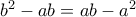 που καταλήγει στο
που καταλήγει στο  , άτοπο.
, άτοπο.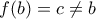 τότε
τότε  . Με παρόμοιο τρόπο όπως στην προηγούμενη παράγραφο καταλήγω σε άτοπο. (Παίρνω τις σχέσεις για
. Με παρόμοιο τρόπο όπως στην προηγούμενη παράγραφο καταλήγω σε άτοπο. (Παίρνω τις σχέσεις για 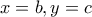 και μετά για
και μετά για 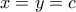 .)
.) για κάθε
για κάθε  .
.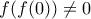 . Σε αυτήν την περίπτωση έχουμε και
. Σε αυτήν την περίπτωση έχουμε και 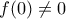 . Θα δείξω ότι
. Θα δείξω ότι 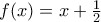 για κάθε
για κάθε 
 παίρνω
παίρνω 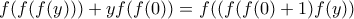
 . Αυτό δίνει ότι η
. Αυτό δίνει ότι η  είναι 1-1 αφού αν
είναι 1-1 αφού αν 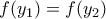 εύκολα καταλήγω σε
εύκολα καταλήγω σε 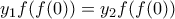 που δίνει
που δίνει  .
. στην αρχική τώρα, και χρησιμοποιώντας ότι η
στην αρχική τώρα, και χρησιμοποιώντας ότι η  είναι 1-1 παίρνω
είναι 1-1 παίρνω 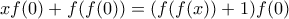 που δίνει
που δίνει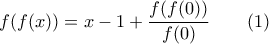
 . Από την (1) παίρνω ότι η
. Από την (1) παίρνω ότι η  είναι επί. Επίσης για
είναι επί. Επίσης για  παίρνω
παίρνω 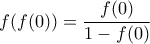
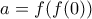 η (1) γίνεται
η (1) γίνεται 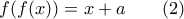
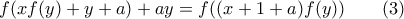
 .
.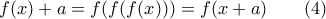
 .
.  είναι επί, μπορώ να πάρω
είναι επί, μπορώ να πάρω  ώστε
ώστε 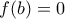 . Για
. Για 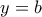 στην (3) παίρνουμε
στην (3) παίρνουμε 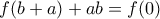 . Όμως από την (4) είναι
. Όμως από την (4) είναι 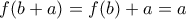 . Άρα
. Άρα 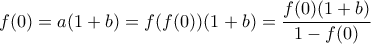
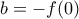 . Τότε όμως έχουμε
. Τότε όμως έχουμε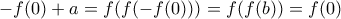
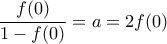
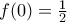 και
και 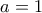 .
.  στην (3) παίρνουμε
στην (3) παίρνουμε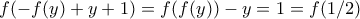
 είναι 1-1 καταλήγουμε στο
είναι 1-1 καταλήγουμε στο 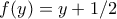 για κάθε
για κάθε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες