Για
 θετικούς πραγματικούς αριθμούς τέτοιους ώστε
θετικούς πραγματικούς αριθμούς τέτοιους ώστε 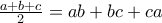
να δειχθεί ότι
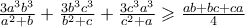
Συντονιστές: achilleas, emouroukos, silouan
Ισοδύναμα, αρκεί να δείξω ότι:
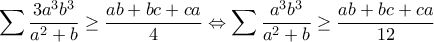
 δίνει:
δίνει: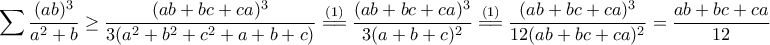
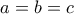 . Αντικαθιστώντας στην
. Αντικαθιστώντας στην  , παίρνουμε
, παίρνουμε 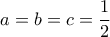 .
.Νομίζω πως Andreescu λειτουργεί αν στους αριθμητές του αθροίσματος έχουμε τετράγωνα..διορθωσέ με αν κάνω λάθος.
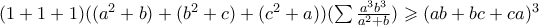
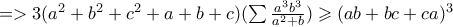
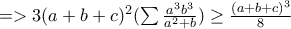
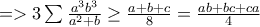
Η Andreescu ισχύει στην γενικευμένη της μορφή ως εξής:
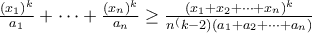
Δεν γνώριζα τη γενίκευση...ευχαριστώ !!Κυριάκος Τσουρέκας έγραψε: ↑Δευ Νοέμ 07, 2022 9:04 pmΗ Andreescu ισχύει στην γενικευμένη της μορφή ως εξής:
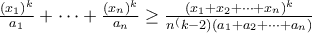
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης