Επιτρέψτε μου να ζητήσω την ενασχόληση με την απόδειξη του Θεωρήματος McLaurin της Ευκλείδειας Γεωμετρίας που είναι πολύ σημαντικό και τουλάχιστον θα πρέπει να το γνωρίζουμε, αφού υπάρχουν περιπτώσεις που «λύνει τα χέρια» του λύτη. Είναι το θεώρημα που ακολουθεί:
«Δίνεται γωνία
 Στις πλευρές της
Στις πλευρές της  κινούνται αντίστοιχα τα σημεία
κινούνται αντίστοιχα τα σημεία  , έτσι ώστε
, έτσι ώστε  όπου
όπου  δοθέν ευθύγραμμο τμήμα και
δοθέν ευθύγραμμο τμήμα και  μέτρα δοθέντων ευθύγραμμων τμημάτων. Τότε ο περιγεγραμμένος κύκλος στο τρίγωνο
μέτρα δοθέντων ευθύγραμμων τμημάτων. Τότε ο περιγεγραμμένος κύκλος στο τρίγωνο  διέρχεται από σταθερό σημείο
διέρχεται από σταθερό σημείο  »
» Παρατήρηση: Αν
 τότε το σταθερό σημείο
τότε το σταθερό σημείο  θα είναι σημείο της διχοτόμου της δοθείσας γωνίας
θα είναι σημείο της διχοτόμου της δοθείσας γωνίας 
Στη περίπτωση μάλιστα που έχουμε
 ισχύει:
ισχύει: 

 σημείο
σημείο  ώστε
ώστε  οπότε το
οπότε το  τον κύκλο που διέρχεται
τον κύκλο που διέρχεται  στο
στο  Ο κύκλος
Ο κύκλος 


 και
και  O λόγος αυτός είναι λοιπόν
O λόγος αυτός είναι λοιπόν  ενώ στην περίπτωση του αθροίσματος το
ενώ στην περίπτωση του αθροίσματος το 
 όπου
όπου


 τα σημεία.
τα σημεία.

 (1)
(1)
 θα είναι
θα είναι  (2)
(2) θα είναι
θα είναι  (3)
(3)
 πρέπει να είναι
πρέπει να είναι 






 τότε
τότε 


 και η άλλη η ευθεία με μιγαδική εξίσωση
και η άλλη η ευθεία με μιγαδική εξίσωση  , με
, με  .
. τότε
τότε  . Κάνουμε αντιστροφή στον μοναδιαίο κύκλο και παίρνουμε
. Κάνουμε αντιστροφή στον μοναδιαίο κύκλο και παίρνουμε  και
και  . Επίσης το
. Επίσης το  πάει στο άπειρο οπότε ο περιγεγραμμένος κύκλος του τριγώνου
πάει στο άπειρο οπότε ο περιγεγραμμένος κύκλος του τριγώνου  πάει στην ευθεία
πάει στην ευθεία  με εξίσωση
με εξίσωση

 για τις στήλες του πίνακα θα έχουμε
για τις στήλες του πίνακα θα έχουμε 
 είναι ανεξάρτητο του
είναι ανεξάρτητο του  και άρα ανήκει στην εικόνα κάθε περιγεγραμμένου κύκλου. Άρα όλοι οι περιγεγγραμμένοι κύκλοι περνάνε από σταθερό σημείο, το οποίο μάλιστα είναι η εικόνα του
και άρα ανήκει στην εικόνα κάθε περιγεγραμμένου κύκλου. Άρα όλοι οι περιγεγγραμμένοι κύκλοι περνάνε από σταθερό σημείο, το οποίο μάλιστα είναι η εικόνα του  που αντιστοιχούν στις περιπτώσεις
που αντιστοιχούν στις περιπτώσεις  αντίστοιχα θα μπορούσαν να αγνοηθούν αλλά πρέπει να εξετάσουμε ξεχωριστά την περίπτωση
αντίστοιχα θα μπορούσαν να αγνοηθούν αλλά πρέπει να εξετάσουμε ξεχωριστά την περίπτωση  . Τότε η γωνία
. Τότε η γωνία  είναι σταθερή. Άρα και η εφαπτομένη του περιγεγραμμένου κύκλου στο
είναι σταθερή. Άρα και η εφαπτομένη του περιγεγραμμένου κύκλου στο  .
. ως τον γεωμετρικό τόπο των σημείων που ο λόγος των αποστάσεων τους από τις
ως τον γεωμετρικό τόπο των σημείων που ο λόγος των αποστάσεων τους από τις  Αυτό μας οδηγεί στο ότι το τρίγωνο
Αυτό μας οδηγεί στο ότι το τρίγωνο  διατηρεί τις γωνίες του. Τελικά καθ’ όλη τη κίνηση το τρίγωνο αυτό μένει όμοιο προς τον εαυτό του. Άρα ο λόγος
διατηρεί τις γωνίες του. Τελικά καθ’ όλη τη κίνηση το τρίγωνο αυτό μένει όμοιο προς τον εαυτό του. Άρα ο λόγος  είναι σταθερός. Από το θεώρημα του Πτολεμαίου έχουμε:
είναι σταθερός. Από το θεώρημα του Πτολεμαίου έχουμε: 
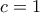 . Ακολουθεί γεωμετρική απόδειξη την οποία δεν είδα πουθενά.
. Ακολουθεί γεωμετρική απόδειξη την οποία δεν είδα πουθενά.  . Επίσης γράφουμε τον (κόκκινο) κύκλο που εφάπτεται της
. Επίσης γράφουμε τον (κόκκινο) κύκλο που εφάπτεται της  . Aν οι δύο αυτοί κύκλοι τέμνονται στο
. Aν οι δύο αυτοί κύκλοι τέμνονται στο  και
και  (υπό χορδής και εφαπτομένης). Άρα τα τρίγωνα
(υπό χορδής και εφαπτομένης). Άρα τα τρίγωνα  είναι όμοια οπότε
είναι όμοια οπότε  (αφού
(αφού  ).
). . Γράφουμε τον κύκλο που διέρχεται από τα σημεία
. Γράφουμε τον κύκλο που διέρχεται από τα σημεία  και έστω ότι τέμνει την
και έστω ότι τέμνει την  δηλαδή
δηλαδή  . Αν το κάνουμε αυτό θα έχουμε τελειώσει γιατί οι κύκλοι προσδιορίζονται από τρία σημεία τους, οπότε ο
. Αν το κάνουμε αυτό θα έχουμε τελειώσει γιατί οι κύκλοι προσδιορίζονται από τρία σημεία τους, οπότε ο  είναι όμοια (άμεσο από γωνίες, π.χ. οι πράσινες είναι ίσες από το εγγράψιμο
είναι όμοια (άμεσο από γωνίες, π.χ. οι πράσινες είναι ίσες από το εγγράψιμο  ). Άρα
). Άρα  αφού
αφού  , όπως θέλαμε. Τελειώσαμε.
, όπως θέλαμε. Τελειώσαμε.  Η δοθείσα σχέση γίνεται
Η δοθείσα σχέση γίνεται 
 με
με  και θεωρούμε
και θεωρούμε  με την ημιευθεία
με την ημιευθεία 

 Επί του ευθύγραμμου τμήματος
Επί του ευθύγραμμου τμήματος  κινείται σημείο
κινείται σημείο  Θεωρούμε σημεία
Θεωρούμε σημεία  , ώστε
, ώστε  Προσδιορίστε τη θέση του
Προσδιορίστε τη θέση του  , ώστε το
, ώστε το  να είναι ελάχιστο.
να είναι ελάχιστο. για οικονομία στις πράξεις). Οι κύκλοι
για οικονομία στις πράξεις). Οι κύκλοι  στις δύο ευθείες, αντίστοιχα, με
στις δύο ευθείες, αντίστοιχα, με  από τα οποία φέρνουμε παράλληλες προς τις πλευρές της γωνίας. Έστω ότι τέμνονται στο
από τα οποία φέρνουμε παράλληλες προς τις πλευρές της γωνίας. Έστω ότι τέμνονται στο  . Θα δείξουμε ότι όλες οι (αντίστροφες) ευθείες διέρχονται από το
. Θα δείξουμε ότι όλες οι (αντίστροφες) ευθείες διέρχονται από το  , όπου
, όπου  . Έστω ακόμα
. Έστω ακόμα  τα αντίστροφα των
τα αντίστροφα των  , αντίστοιχα, δηλαδή
, αντίστοιχα, δηλαδή  και
και  . Θέλουμε να δείξουμε ότι τα
. Θέλουμε να δείξουμε ότι τα  είναι συνευθειακά. Αν λοιπόν η
είναι συνευθειακά. Αν λοιπόν η  τέμνει την κάτω πλευρά της γωνίας στο
τέμνει την κάτω πλευρά της γωνίας στο 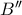 έχουμε από τα όμοια τρίγωνα
έχουμε από τα όμοια τρίγωνα  ότι
ότι  , δηλαδή
, δηλαδή  .
.  , όπως θέλαμε.
, όπως θέλαμε.  ότι
ότι