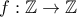 τέτοιες ώστε
τέτοιες ώστε 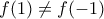 και
και 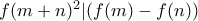 για όλους τους
για όλους τους 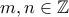 .
.Παρατήρηση.
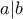 σημαίνει ότι υπάρχει ακέραιος
σημαίνει ότι υπάρχει ακέραιος  τέτοιος ώστε
τέτοιος ώστε 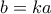 . Για παράδειγμα,
. Για παράδειγμα, 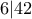 ,
, 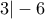 ,
, 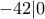 και
και 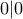 .
. Φιλικά,
Αχιλλέας
Συντονιστές: achilleas, emouroukos, silouan
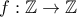 τέτοιες ώστε
τέτοιες ώστε 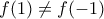 και
και 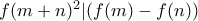 για όλους τους
για όλους τους 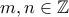 .
.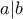 σημαίνει ότι υπάρχει ακέραιος
σημαίνει ότι υπάρχει ακέραιος  τέτοιος ώστε
τέτοιος ώστε 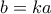 . Για παράδειγμα,
. Για παράδειγμα, 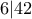 ,
, 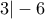 ,
, 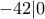 και
και 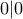 .
. 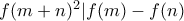 ?
? θα είναι
θα είναι 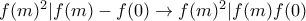
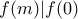
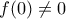 , θα είναι f σταθερή , αλλά αν
, θα είναι f σταθερή , αλλά αν 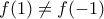 , δεν μπορεί f να είναι σταθερή
, δεν μπορεί f να είναι σταθερή  που μας οδηγεί στο
που μας οδηγεί στο 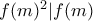 δηλαδή
δηλαδή 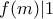 πάλι f constant
πάλι f constant 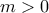 είναι
είναι  και για κάθε
και για κάθε 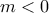 ,
, 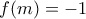
Καλησπέρα σας. Νομίζω δεν γίνεται
 διότι για
διότι για 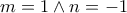 έχουμε:
έχουμε: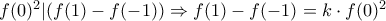 , όπου
, όπου 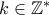 . Οπότε από υπόθεση πρέπει
. Οπότε από υπόθεση πρέπει 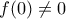 .
.Έχουμε
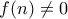 για κάθε
για κάθε  .
. με
με 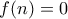 , τότε από τη συναρτησιακή για
, τότε από τη συναρτησιακή για 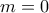 θα είχαμε
θα είχαμε 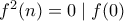 , άρα
, άρα  που δεν γίνεται όπως είπε η Μαριλένα.
που δεν γίνεται όπως είπε η Μαριλένα.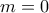 , παίρνουμε
, παίρνουμε 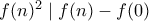 .
. με
με 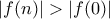 .
.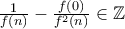 και
και 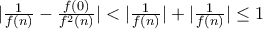 .
.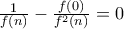 , οπότε
, οπότε 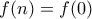 άτοπο.
άτοπο.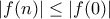 για κάθε
για κάθε  .
.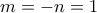 . Άρα
. Άρα 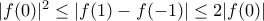 , επειδή
, επειδή 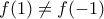 από την συναρτησιακή.
από την συναρτησιακή.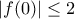 .
.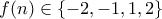 .
.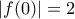 . Άρα
. Άρα 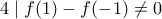 , οπότε
, οπότε 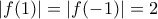 .
.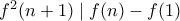 και
και 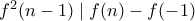 .
.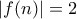 η
η 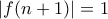 και επίσης
και επίσης 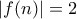 η
η 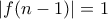 .
.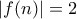 τότε
τότε 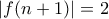 και επίσης αν
και επίσης αν 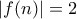 τότε
τότε 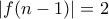 .
.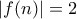 για κάθε
για κάθε 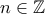 .
.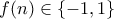 με
με 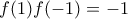 και οι
και οι 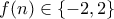 με
με 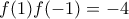 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες