 οι οποίες είναι τέτοιες, ώστε
οι οποίες είναι τέτοιες, ώστε
Συντονιστές: achilleas, emouroukos, silouan
 οι οποίες είναι τέτοιες, ώστε
οι οποίες είναι τέτοιες, ώστε
 για κάθε
για κάθε  και
και  για κάθε
για κάθε  οι οποίες προφανώς ικανοποιούν τη σχέση.
οι οποίες προφανώς ικανοποιούν τη σχέση. με
με 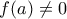 .
. 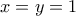 έχουμε
έχουμε 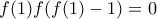 άρα
άρα  ή
ή 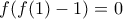 . Σε κάθε περίπτωση υπάρχει
. Σε κάθε περίπτωση υπάρχει  ώστε
ώστε 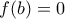 . Για
. Για 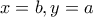 παίρνω
παίρνω 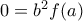 και άρα
και άρα 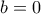 .
.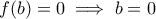 και αφού
και αφού  ή
ή 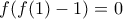 , τότε έχουμε και
, τότε έχουμε και  . Για
. Για  παίρνω
παίρνω 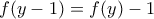 για κάθε
για κάθε 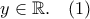
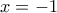 στην (1) παίρνουμε
στην (1) παίρνουμε 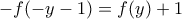 και επειδή
και επειδή 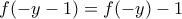 από την (1) παίρνουμε
από την (1) παίρνουμε 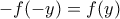 , δηλαδή η
, δηλαδή η  είναι περιττή.
είναι περιττή.![\displaystyle x^2f(y) - f(x) = f(x)f(yf(x)-1) = f(x)[f(yf(x)) - 1] \displaystyle x^2f(y) - f(x) = f(x)f(yf(x)-1) = f(x)[f(yf(x)) - 1]](/forum/ext/geomar/texintegr/latexrender/pictures/011b0f015a1742d93eb3c1e8c377d1f7.png) οπότε
οπότε 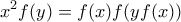 για κάθε
για κάθε 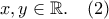
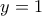 στη (2) παίρνω
στη (2) παίρνω 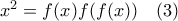
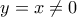 παίρνω
παίρνω 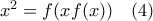 η οποία ισχύει προφανώς και για
η οποία ισχύει προφανώς και για 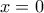 .
. περιέχει το
περιέχει το 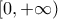 και επειδή η
και επειδή η  είναι περιττή, θα είναι και επί. Αντικαθιστώντας της (3) στη (2) και διαιρώντας με
είναι περιττή, θα είναι και επί. Αντικαθιστώντας της (3) στη (2) και διαιρώντας με  για
για  παίρνουμε
παίρνουμε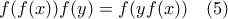
 . Επειδή η
. Επειδή η  είναι επί για κάθε
είναι επί για κάθε  θα υπάρχει
θα υπάρχει 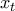 με
με 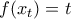 και για
και για 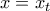 στην (5) έχουμε
στην (5) έχουμε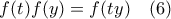
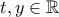
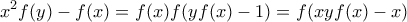
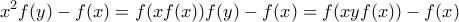
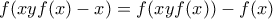 που για
που για 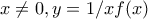 γίνεται
γίνεται 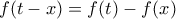 . Άρα, αφού η
. Άρα, αφού η  είναι και περιττή, παίρνουμε ότι η
είναι και περιττή, παίρνουμε ότι η  είναι προσθετική (ικανοποιεί τη συναρτησιακή του Cauchy). Επειδή είναι και πολλαπλασιαστική (ικανοποιεί την (6)) τότε είτε είναι ταυτοτική
είναι προσθετική (ικανοποιεί τη συναρτησιακή του Cauchy). Επειδή είναι και πολλαπλασιαστική (ικανοποιεί την (6)) τότε είτε είναι ταυτοτική  είτε είναι η ταυτοτική συνάρτηση.
είτε είναι η ταυτοτική συνάρτηση.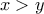 θέτω
θέτω 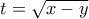 . Τότε
. Τότε 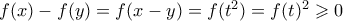 . Άρα η
. Άρα η  είναι μονότονη και αφού ικανοποιεί την Cauchy θα είναι της μορφής
είναι μονότονη και αφού ικανοποιεί την Cauchy θα είναι της μορφής 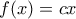 για κάποιο
για κάποιο  (γνωστό). Επειδή
(γνωστό). Επειδή 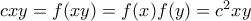 παίρνουμε
παίρνουμε  ή
ή 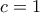 .
.Καλησπέρα σε όλους. Ευχαριστώ τον κ. Δημήτρη για την λύση. Η πηγή της άσκησης είναι από το Topics in Functional Equations των Andreescu, Boreico, Mushkarov και Nikolov (κεφάλαιο 3, πρόβλημα 3.18). Η λύση μου είναι, περιληπτικά, η εξής:Ορέστης Λιγνός έγραψε: ↑Τετ Νοέμ 01, 2023 8:53 pmΝα βρείτε όλες τις συναρτήσειςοι οποίες είναι τέτοιες, ώστε

 δεν είναι η μηδενική συνάρτηση.
δεν είναι η μηδενική συνάρτηση. και
και  . Πράγματι, με
. Πράγματι, με  στην αρχική προκύπτει ότι
στην αρχική προκύπτει ότι 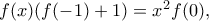 και άρα αν
και άρα αν 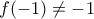 τότε
τότε 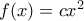 με
με  σταθερά, κάτι το οποίο εύκολα απορρίπτεται. Συνεπώς
σταθερά, κάτι το οποίο εύκολα απορρίπτεται. Συνεπώς  και, με
και, με  προκύπτει
προκύπτει  .
.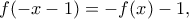
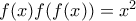 και
και 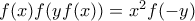 . Πράγματι, για την πρώτη σχέση αρκεί να πάρουμε
. Πράγματι, για την πρώτη σχέση αρκεί να πάρουμε  στην αρχική.
στην αρχική. 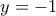 προκύπτει ότι
προκύπτει ότι 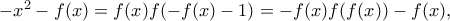 άρα
άρα 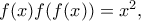 όπως θέλαμε.
όπως θέλαμε.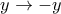 η αρχική δίνει ότι
η αρχική δίνει ότι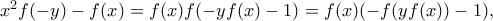
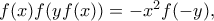 όπως θέλαμε.
όπως θέλαμε. επί. Πράγματι, από την
επί. Πράγματι, από την 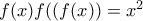 προκύπτει ότι
προκύπτει ότι  αν και μόνο αν
αν και μόνο αν  , συνεπώς για
, συνεπώς για  και
και  στην αρχική παίρνουμε ότι
στην αρχική παίρνουμε ότι 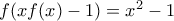 , και άρα
, και άρα 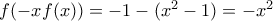 . Επομένως, η
. Επομένως, η  παίρνει κάθε τιμή στο
παίρνει κάθε τιμή στο ![(-\infty, 0], (-\infty, 0],](/forum/ext/geomar/texintegr/latexrender/pictures/de374b22d4bcc6ac9aeb6e0a44961e18.png) και αφού
και αφού 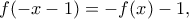 παίρνει και κάθε τιμή στο
παίρνει και κάθε τιμή στο  .
.  . Είναι,
. Είναι, 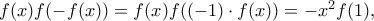 και άρα αφού
και άρα αφού 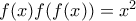 και η
και η  είναι επί, διαιρώντας κατά μέλη πρέπει
είναι επί, διαιρώντας κατά μέλη πρέπει 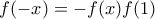 για κάθε
για κάθε  .
. προκύπτει ότι
προκύπτει ότι 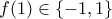 . Αν όμως
. Αν όμως 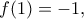 τότε
τότε 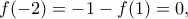 άτοπο.
άτοπο.  είναι η ταυτοτική συνάρτηση. Πράγματι, από τα παραπάνω προκύπτει ότι η
είναι η ταυτοτική συνάρτηση. Πράγματι, από τα παραπάνω προκύπτει ότι η  είναι περιττή, και άρα
είναι περιττή, και άρα 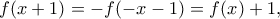 συνεπώς
συνεπώς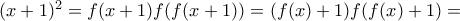
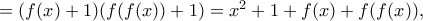
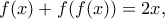 και αφού
και αφού 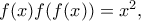 προκύπτει εύκολα ότι
προκύπτει εύκολα ότι 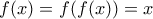 για κάθε
για κάθε  .
.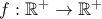 οι οποίες είναι τέτοιες, ώστε
οι οποίες είναι τέτοιες, ώστε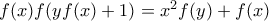
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης