 τα ύψη οξυγώνιου τριγώνου
τα ύψη οξυγώνιου τριγώνου  ,
,  το ορθόκεντρο και
το ορθόκεντρο και  το μέσο του
το μέσο του  . Οι περίκυκλοι των
. Οι περίκυκλοι των τριγώνων
 τέμνονται στα σημεία
τέμνονται στα σημεία  (το
(το  στο ίδιο μέρος με το
στο ίδιο μέρος με το  ως προς την
ως προς την  ). Να δείξετε ότι
). Να δείξετε ότι οι ευθείες
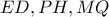 τέμνονται πάνω στον περίκυκλο του
τέμνονται πάνω στον περίκυκλο του 
Συντονιστές: vittasko, silouan, rek2
 τα ύψη οξυγώνιου τριγώνου
τα ύψη οξυγώνιου τριγώνου  ,
,  το ορθόκεντρο και
το ορθόκεντρο και  το μέσο του
το μέσο του  . Οι περίκυκλοι των
. Οι περίκυκλοι των  τέμνονται στα σημεία
τέμνονται στα σημεία  (το
(το  στο ίδιο μέρος με το
στο ίδιο μέρος με το  ως προς την
ως προς την  ). Να δείξετε ότι
). Να δείξετε ότι 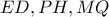 τέμνονται πάνω στον περίκυκλο του
τέμνονται πάνω στον περίκυκλο του 
george visvikis έγραψε:Έστωτα ύψη οξυγώνιου τριγώνου
,
το ορθόκεντρο και
το μέσο του
. Οι περίκυκλοι των τριγώνων
τέμνονται στα σημεία
(το
στο ίδιο μέρος με το
ως προς την
). Να δείξετε ότι οι ευθείες
τέμνονται πάνω στον περίκυκλο του
 Έστω
Έστω  (με
(με  τον περίκυκλο του τριγώνου
τον περίκυκλο του τριγώνου  ) εκατέρωθεν του
) εκατέρωθεν του  ως προς την
ως προς την  και ας είναι
και ας είναι  τα σημεία τομής των
τα σημεία τομής των 
 του τριγώνου
του τριγώνου  αντίστοιχα (με
αντίστοιχα (με  μεταξύ
μεταξύ  και
και  ) . Αρκεί να δείξουμε ισοδύναμα ότι
) . Αρκεί να δείξουμε ισοδύναμα ότι  είναι σημεία του μεσόκυκλου
είναι σημεία του μεσόκυκλου 
 . Έστω
. Έστω  τα σημεία τομής των
τα σημεία τομής των  με τους κύκλους
με τους κύκλους  αντίστοιχα (με
αντίστοιχα (με  ).
).  Είναι
Είναι 

 ομοκυκλικά, άρα
ομοκυκλικά, άρα  :(1).
:(1). τότε για τις τεμνόμενες στο
τότε για τις τεμνόμενες στο  χορδές
χορδές  του
του  θα ισχύει:
θα ισχύει: 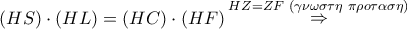


 το μέσο της
το μέσο της  .
. Είναι γνωστό ότι ο μεσόκυκλος
Είναι γνωστό ότι ο μεσόκυκλος  του
του  έχει κέντρο το μέσο του
έχει κέντρο το μέσο του  (το τμήμα που συνδέει το ορθόκεντρο με το βαρύκεντρο του τριγώνου
(το τμήμα που συνδέει το ορθόκεντρο με το βαρύκεντρο του τριγώνου  ) και ακτίνα
) και ακτίνα  .
.
 .
. Το μέσο
Το μέσο  της κοινής χορδής
της κοινής χορδής  των ίσων κύκλων
των ίσων κύκλων  (τα
(τα  αποτελούν ορθοκεντρική τετράδα και ως γνωστό οι περίκυκλοι των τεσσάρων τριγώνων κάθε ορθοκεντρικής τετράδας είναι ίσοι)
αποτελούν ορθοκεντρική τετράδα και ως γνωστό οι περίκυκλοι των τεσσάρων τριγώνων κάθε ορθοκεντρικής τετράδας είναι ίσοι)  . Για τις τεμνόμενες στο
. Για τις τεμνόμενες στο  χορδές
χορδές 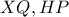 του
του  ισχύει:
ισχύει: 


 ομοκυκλικά.
ομοκυκλικά. Από το τρίγωνο
Από το τρίγωνο 
 .
. . Από
. Από  το ισοδύναμο πρόβλημα έχει αποδειχθεί.
το ισοδύναμο πρόβλημα έχει αποδειχθεί. τότε
τότε  άρα
άρα  εγγράψιμο οπότε
εγγράψιμο οπότε  άρα και
άρα και  εγγράψιμο οπότε είναι
εγγράψιμο οπότε είναι 
 οπότε
οπότε  εγγράψιμο. (*)
εγγράψιμο. (*) και ακτίνας
και ακτίνας  διατηρεί σταθερά τα σημεία
διατηρεί σταθερά τα σημεία  και ο κύκλος
και ο κύκλος  γίνεται η ευθεία
γίνεται η ευθεία  Επιπλέον έστω
Επιπλέον έστω  η τομή της ημιευθείας
η τομή της ημιευθείας  με τον κύκλο
με τον κύκλο  τότε είναι απλό ότι
τότε είναι απλό ότι  οπότε ο κύκλος
οπότε ο κύκλος  γίνεται ο κύκλος
γίνεται ο κύκλος  και συνεπώς η εικόνα του
και συνεπώς η εικόνα του  θα είναι η τομή της ημιευθείας
θα είναι η τομή της ημιευθείας 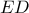 με τον κύκλο
με τον κύκλο  δηλαδή το
δηλαδή το  Σωνεπώς τα σημεία
Σωνεπώς τα σημεία  είναι συνευθειακά.
είναι συνευθειακά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες