 και ας είναι
και ας είναι  τα σημεία επαφής του εγγεγραμμένου του κύκλου
τα σημεία επαφής του εγγεγραμμένου του κύκλου  με τις πλευρές
με τις πλευρές  αντίστοιχα. Αν
αντίστοιχα. Αν  είναι το σημείο τομής της
είναι το σημείο τομής της  με την κάθετη στην
με την κάθετη στην  στο σημείο επαφής (έστω
στο σημείο επαφής (έστω  ) του
) του 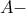 παρεγγεραμμένου κύκλου
παρεγγεραμμένου κύκλου  με την
με την  να δειχθεί ότι ο περίκυκλος του τριγώνου
να δειχθεί ότι ο περίκυκλος του τριγώνου  εφάπτεται της
εφάπτεται της  , όπου
, όπου  είναι η ορθή προβολή του μέσου
είναι η ορθή προβολή του μέσου  της
της  επί της
επί της 
Στάθης

 η προβολή του
η προβολή του  στην
στην  η προβολή του
η προβολή του  το έγκεντρο του
το έγκεντρο του  . Ισχύει
. Ισχύει  (επειδή
(επειδή  ).
). 

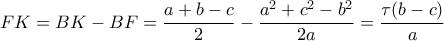
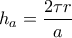
 (επειδή
(επειδή  ).
). και αφού
και αφού  έχουμε
έχουμε  .
.  και τα
και τα  είναι όμοια. Άρα
είναι όμοια. Άρα  και ο κύκλος
και ο κύκλος  εφάπτεται στην
εφάπτεται στην