ΕΧΕΙ ΞΑΝΑΤΕΘΕΙ ΑΛΛΙΩΣ...

ΚΕΦΑΛΟΝΙΤΗΣ · #1

Η ανισότητα που προτείνω έχει τεθεί κάπως διαφορετικά...
Ας τη δούμε από μια άλλη σκοπιά...

Σε τρίγωνο ABC

αποδείξτε ότι
$\displaystyle cos^{2}\frac{A}{2}+cos^{2}\frac{B}{2}+cos^{2}\frac{C}{2}\geq \frac{\sqrt{3}s}{2R}$

#2

Είναι:

$\displaystyle{{\cos ^2}\frac{A}{2} + {\cos ^2}\frac{B}{2} + {\cos ^2}\frac{C}{2} = \frac{1}{2}\left( {\cos A + \cos B + \cos C + 3} \right) = \frac{1}{2}\left( {\frac{{R + r}}{R} + 3} \right) = \frac{{4R + r}}{{2R}}.}$

Το ζητούμενο προκύπτει άμεσα από την ανισότητα Finsler-Hadwiger $\displaystyle{4R + r \ge \sqrt 3 s,}$ η οποία έχει συζητηθεί πολλές φορές στο

.

Διονύσιος Αδαμόπουλος · #3

ΚΕΦΑΛΟΝΙΤΗΣ έγραψε:Η ανισότητα που προτείνω έχει τεθεί κάπως διαφορετικά...
Ας τη δούμε από μια άλλη σκοπιά...

Σε τρίγωνο αποδείξτε ότι
$\displaystyle cos^{2}\frac{A}{2}+cos^{2}\frac{B}{2}+cos^{2}\frac{C}{2}\geq \frac{\sqrt{3}s}{2R}$

Μια άλλη ελπίζω σωστή αντιμετώπιση:

$\cos^{2}\dfrac{A}{2}+\cos^{2}\dfrac{B}{2}+\cos^{2}\dfrac{C}{2}\geq \dfrac{\sqrt{3}s}{2R}\Leftrightarrow$ $3\cos^{2}\dfrac{A}{2}+3\cos^{2}\dfrac{B}{2}+3\cos^{2}\dfrac{C}{2}\geq \dfrac{3\sqrt{3}s}{2R}$

Όμως ισχύει ότι: $3(\cos^{2}\dfrac{A}{2}+\cos^{2}\dfrac{B}{2}+\cos^{2}\dfrac{C}{2})\geq$ $(\cos \dfrac{A}{2}+\cos \dfrac{B}{2}+\cos \dfrac{C}{2})^2$

Αρκεί λοιπόν:

$(\cos \dfrac{A}{2}+\cos \dfrac{B}{2}+\cos \dfrac{C}{2})^2\geq \dfrac{3\sqrt{3}s}{2R}$ (1)

Γνωρίζουμε πως η συνάρτηση $f(x)=\sin x$ είναι κοίλη στις γωνίες που μας αφορούν.

Από την ανισότητα Popoviciou

λοιπόν παίρνουμε ότι:

$2(\sin \dfrac{A+B}{2} + \sin \dfrac{B+C}{2}+\sin \dfrac{C+A}{2})\geq \sin A+\sin B+\sin C+3(\sin \dfrac{A+B+C}{3})$ $\Leftrightarrow 2(\cos \dfrac{A}{2} + \cos \dfrac{B}{2}+\cos \dfrac{C}{2})\geq$ $\sin A+\sin B+\sin C+\dfrac{3\sqrt{3}}{2}$

Από νόμο τον ημιτόνων έχουμε ότι:

$\sin A+\sin B+\sin C=\dfrac{a}{2R}+\dfrac{b}{2R}+\dfrac{c}{2R}=\dfrac{2s}{2R}$

Επομένως έχουμε ότι:

$2(\cos \dfrac{A}{2} + \cos \dfrac{B}{2}+\cos \dfrac{C}{2})\geq \dfrac{2s}{2R}+\dfrac{3\sqrt{3}}{2}\Leftrightarrow$ $\cos \dfrac{A}{2} + \cos \dfrac{B}{2}+\cos \dfrac{C}{2}\geq \dfrac{2s+3\sqrt{3}R}{4R}\Leftrightarrow$ $(\cos \dfrac{A}{2} + \cos \dfrac{B}{2}+\cos \dfrac{C}{2})^2\geq \dfrac{(2s+3\sqrt{3}R)^2}{16R^2}$

Για να ισχύει λοιπόν η (1) αρκεί:

$\dfrac{(2s+3\sqrt{3}R)^2}{16R^2}\geq \dfrac{3\sqrt{3}s}{2R}\Leftrightarrow$ $(2s+3\sqrt{3}R)^2\geq 24R\sqrt{3}s$

Αν θέσουμε όπου

και $3\sqrt{3}R$ τα

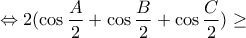
και

αντίστοιχα η ανισότητα γίνεται:

$(x+y)^2\geq 4xy$ που ισχύει.

ΚΕΦΑΛΟΝΙΤΗΣ · #4

Να ευχαριστήσω το Βαγγέλη Μουρούκο και το Διονύση Αδαμόπουλο για τις λύσεις τους.
Ας δούμε τις δικές μου σκέψεις...

Οφείλω να παραδεχτώ ότι η λύση μου είναι κάπως '' ετοιματζίδικη ''...
Η λύση μου βασίζεται στην παρακάτω δημοσίευση
viewtopic.php?f=112&t=24551
Το θέμα εκείνο δεν ήταν κάτι άλλο παρά η ανισότητα Weitzenböck στο τρίγωνο EDF.

Aν ληφθεί υπ' όψιν ότι
$\displaystyle{DE = 4R\cos \frac{C}{2}}$

$\displaystyle{EF = 4R\cos \frac{A}{2}}$

$\displaystyle{FD = 4R\cos \frac{B}{2}}$

και ότι (EDF)=2sR

η ανισότητα αυτή γράφεται

$\displaystyle\left ( { 4R\cos \frac{A}{2}} \right )^{2}+\left ( { 4R\cos \frac{B}{2}} \right )^{2}+\left ( { 4R\cos \frac{A}{2}} \right )^{2}\geq 4\sqrt{3}\cdot 2sR$

που είναι ισοδύναμη με

$\displaystyle16R^{2}\left ( cos^{2}\frac{A}{2}+ cos^{2}\frac{B}{2}+cos^{2}\frac{C}{2}\right )\geq 4\sqrt{3}\cdot 2sR$

η οποία είναι προφανώς ισοδύναμη με την

$\displaystyle cos^{2}\frac{A}{2}+ cos^{2}\frac{B}{2}+cos^{2}\frac{C}{2}\geq \frac{\sqrt{3}s}{2R}$

#5

ΚΕΦΑΛΟΝΙΤΗΣ έγραψε:
Σε τρίγωνο αποδείξτε ότι
$\displaystyle cos^{2}\frac{A}{2}+cos^{2}\frac{B}{2}+cos^{2}\frac{C}{2}\geq \frac{\sqrt{3}s}{2R}$

Λίγο διαφορετικά...

Ισχύουν: $\displaystyle E=r_{a}(s-a),\,\,\,\,\ r_{a}+r_{b}+r_{c}=4R+r\geq \sqrt{3}s$

$\displaystyle r_{b}+r_{c}=4R\dfrac{s(s-a)}{bc}=4R\cos^2(\frac{A}{2})\Rightarrow \cos^2(\dfrac{A}{2})=\dfrac{r_{b}+r_{c}}{4R}$

Έτσι $\displaystyle \cos^2(\dfrac{A}{2})+\cos^2(\dfrac{B}{2})+\cos^2(\dfrac{C}{2})=\dfrac{r_{a}+r_{b}+r_{c}}{2R}=\dfrac{4R+r}{2R}\geq \dfrac{\sqrt{3}s}{2R}$

ΕΧΕΙ ΞΑΝΑΤΕΘΕΙ ΑΛΛΙΩΣ...

ΕΧΕΙ ΞΑΝΑΤΕΘΕΙ ΑΛΛΙΩΣ...

Re: ΕΧΕΙ ΞΑΝΑΤΕΘΕΙ ΑΛΛΙΩΣ...

Re: ΕΧΕΙ ΞΑΝΑΤΕΘΕΙ ΑΛΛΙΩΣ...

Re: ΕΧΕΙ ΞΑΝΑΤΕΘΕΙ ΑΛΛΙΩΣ...

Re: ΕΧΕΙ ΞΑΝΑΤΕΘΕΙ ΑΛΛΙΩΣ...

Μέλη σε σύνδεση