 το έγκεντρο και
το έγκεντρο και  η ακτίνα του περίκυκλου τριγώνου
η ακτίνα του περίκυκλου τριγώνου  Στη προέκταση του ύψους
Στη προέκταση του ύψους  θεωρούμε σημείο
θεωρούμε σημείο  ώστε
ώστε  Να δείξετε ότι
Να δείξετε ότι 
Συντονιστές: vittasko, silouan, rek2
 το έγκεντρο και
το έγκεντρο και  η ακτίνα του περίκυκλου τριγώνου
η ακτίνα του περίκυκλου τριγώνου  Στη προέκταση του ύψους
Στη προέκταση του ύψους  θεωρούμε σημείο
θεωρούμε σημείο  ώστε
ώστε  Να δείξετε ότι
Να δείξετε ότι 
 ένα σημείο στην προέκταση της
ένα σημείο στην προέκταση της  ώστε
ώστε 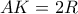 , τότε,
, τότε,  .
. ο κύκλος
ο κύκλος  .
.
 .
. , ή ισοδύναμα ότι η
, ή ισοδύναμα ότι η  εφάπτεται στον κύκλο
εφάπτεται στον κύκλο  , ή αλλιώς ότι
, ή αλλιώς ότι  .
. στον κύκλο
στον κύκλο  , έστω
, έστω  .
. και
και  είναι ίσες (γνωστό λήμμα), και αφού
είναι ίσες (γνωστό λήμμα), και αφού  , έπεται ότι
, έπεται ότι  .
. έχουν
έχουν  , οπότε είναι ίσα, και άρα
, οπότε είναι ίσα, και άρα  .
. .
. .
.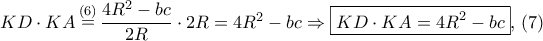 .
. .
.  το κέντρο του κύκλου
το κέντρο του κύκλου  , που είναι και μέσο του
, που είναι και μέσο του  .
. έχουμε
έχουμε 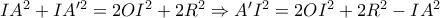 .
. , όπου
, όπου  η ακτίνα του εγκύκλου του
η ακτίνα του εγκύκλου του  .
. .
.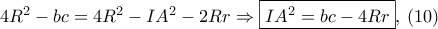 .
. την ημιπερίμετρο του τριγώνου
την ημιπερίμετρο του τριγώνου  )
)  .
. .
. .
. .
. ,
, 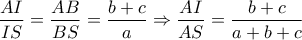 .
.![AS=\sqrt{bc[1-\dfrac{a^2}{(b+c)^2}]} AS=\sqrt{bc[1-\dfrac{a^2}{(b+c)^2}]}](/forum/ext/geomar/texintegr/latexrender/pictures/5bab8131ad6b6094a88ac61dc659f291.png) , οπότε
, οπότε  , οπότε
, οπότε  , και, η (12), δείχτηκε.
, και, η (12), δείχτηκε. το, άλλο, σημείο τομής της
το, άλλο, σημείο τομής της  με το κύκλο και
με το κύκλο και  το αντιδιαμετρικό του
το αντιδιαμετρικό του  ,
,  αφού ως γνωστό η διχοτόμος της γωνίας
αφού ως γνωστό η διχοτόμος της γωνίας  του
του 
 . Θα δείξω τώρα το παρακάτω λήμμα ( έχει συμβατικά
. Θα δείξω τώρα το παρακάτω λήμμα ( έχει συμβατικά  η προβολή του
η προβολή του  στη
στη  ).
). φέρω το ύψος
φέρω το ύψος  , την
, την  του εγγεγραμμένου κύκλου και η
του εγγεγραμμένου κύκλου και η  τέμνει ακόμα τον περιγεγραμμένο κύκλο του
τέμνει ακόμα τον περιγεγραμμένο κύκλο του  στο
στο  , με
, με  το
το  , τότε
, τότε  . Δηλαδή
. Δηλαδή 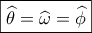 .
. να έχουν ανάλογες κάθετες πλευρές .
να έχουν ανάλογες κάθετες πλευρές . και από το Θ, Πτολεμαίου στο τετράπλευρο
και από το Θ, Πτολεμαίου στο τετράπλευρο  προκύπτει
προκύπτει  και λόγω της ομοιότητας
και λόγω της ομοιότητας 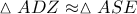 ,
,  . Επειδή τώρα
. Επειδή τώρα 
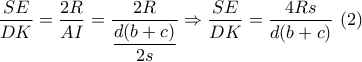 .
. προκύπτει το ζητούμενο του λήμματος .
προκύπτει το ζητούμενο του λήμματος . αντιδιαμετρικό του
αντιδιαμετρικό του  για να «δούμε» το
για να «δούμε» το  . Τότε αν
. Τότε αν  το μέσον του απέναντι από την κορυφή
το μέσον του απέναντι από την κορυφή  τόξου
τόξου  , και
, και  είναι η τομή του ύψους
είναι η τομή του ύψους  με τον κύκλο
με τον κύκλο  και
και  η τομή του ύψους με την
η τομή του ύψους με την  , τότε συμβαίνουν τα εξής:
, τότε συμβαίνουν τα εξής:  ,
, 
 Τα τρίγωνα
Τα τρίγωνα  είναι προφανώς όμοια, άρα ισχύει
είναι προφανώς όμοια, άρα ισχύει  Επομενως τα σημεία
Επομενως τα σημεία 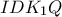 είναι ομοκυκλικά, οπότε
είναι ομοκυκλικά, οπότε Τελικά έχουμε
Τελικά έχουμε 
 και θα δείξω ότι
και θα δείξω ότι 
 το αντιδιαμετρικό του
το αντιδιαμετρικό του  ως προς τον περιγεγραμμένο κύκλο,
ως προς τον περιγεγραμμένο κύκλο,  το
το 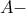 παράκεντρο και
παράκεντρο και  το σημείο τομής της
το σημείο τομής της  με τον κύκλο
με τον κύκλο  Ως γνωστόν
Ως γνωστόν 
 (Θεώρημα του
(Θεώρημα του  ). Τα τρίγωνα
). Τα τρίγωνα  είναι όμοια
είναι όμοια οπότε
οπότε 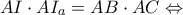




 απ' όπου λόγω ομοιότητας, έπεται το ζητούμενο.
απ' όπου λόγω ομοιότητας, έπεται το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: KDORTSI και 10 επισκέπτες