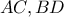 τραπεζίου
τραπεζίου  τέμνονται κάθετα στο
τέμνονται κάθετα στο 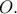 Έστω
Έστω  το συμμετρικό του
το συμμετρικό του  ως προς
ως προςτο μέσο
 της
της  και
και  οι προβολές των
οι προβολές των  αντίστοιχα στην
αντίστοιχα στην  Αν η κάθετη από το
Αν η κάθετη από το  στην
στην  τέμνει την
τέμνει την 
στο
 να δείξετε ότι
να δείξετε ότι 
Συντονιστές: vittasko, silouan, rek2
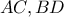 τραπεζίου
τραπεζίου  τέμνονται κάθετα στο
τέμνονται κάθετα στο 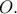 Έστω
Έστω  το συμμετρικό του
το συμμετρικό του  ως προς
ως προς της
της  και
και  οι προβολές των
οι προβολές των  αντίστοιχα στην
αντίστοιχα στην  Αν η κάθετη από το
Αν η κάθετη από το  στην
στην  τέμνει την
τέμνει την 
 να δείξετε ότι
να δείξετε ότι 
 .
.  πάει στο
πάει στο  και αφού
και αφού  , έχουμε ότι η
, έχουμε ότι η  είναι συμμετρική της
είναι συμμετρική της  .
. , έστω
, έστω  , είναι σημείο του
, είναι σημείο του  .
. και
και  είναι συμμετρικά. Άρα οι ευθείες
είναι συμμετρικά. Άρα οι ευθείες  και
και  είναι συμμετρικές, δηλαδή παράλληλες, επομένως
είναι συμμετρικές, δηλαδή παράλληλες, επομένως  .
. έχει συμμετρική την
έχει συμμετρική την  . Αρκεί λοιπόν
. Αρκεί λοιπόν  να είναι κάθετη στην
να είναι κάθετη στην  .
. με τις διαγώνιές του να τέμνονται κάθετα στο
με τις διαγώνιές του να τέμνονται κάθετα στο  . Φέρνουμε κάθετη
. Φέρνουμε κάθετη  στην
στην  . Έστω
. Έστω  η τομή των καθέτων από τα
η τομή των καθέτων από τα  στις
στις  και
και  αντίστοιχα, οι οποίες τέμνουν τις
αντίστοιχα, οι οποίες τέμνουν τις  και
και  στα
στα  . Να αποδειχθεί πως το
. Να αποδειχθεί πως το  ανήκει στην
ανήκει στην  .
. , έχουμε πως το τετράπλευρο
, έχουμε πως το τετράπλευρο  είναι εγγράψιμο σε κύκλο με κέντρο
είναι εγγράψιμο σε κύκλο με κέντρο  (
( είναι το μέσο του
είναι το μέσο του  ).
). εγγράψιμο σε κύκλο με κέντρο
εγγράψιμο σε κύκλο με κέντρο  (
( είναι το μέσο του
είναι το μέσο του  ).
). το δεύτερο σημείο τομής των κύκλων με κέντρα
το δεύτερο σημείο τομής των κύκλων με κέντρα  και
και  . Έχουμε πως το
. Έχουμε πως το 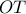 είναι ο ριζικός άξονας των δύο κύκλων, άρα είναι
είναι ο ριζικός άξονας των δύο κύκλων, άρα είναι  .
. , άρα
, άρα  .
. , έχουμε πως και τα σημεία
, έχουμε πως και τα σημεία  είναι συνευθειακά. Άρα το
είναι συνευθειακά. Άρα το  ανήκει στο ριζικό άξονα των δύο κύκλων και ισχύει ότι
ανήκει στο ριζικό άξονα των δύο κύκλων και ισχύει ότι  , άρα το
, άρα το  είναι εγγράψιμο
είναι εγγράψιμο ανήκει στο ριζικό άξονα των δύο κύκλων δηλαδή αρκεί:
ανήκει στο ριζικό άξονα των δύο κύκλων δηλαδή αρκεί: , δηλαδή αρκεί το
, δηλαδή αρκεί το  να είναι εγγράψιμο.
να είναι εγγράψιμο.

 και
και 
 και το ζητούμενο έπεται.
και το ζητούμενο έπεται. Από
Από  , έχουμε ότι το παραλληλλόγραμμο
, έχουμε ότι το παραλληλλόγραμμο 
 από το σημείο
από το σημείο  ως κοινό μέσον των διαγωνίων του
ως κοινό μέσον των διαγωνίων του  είναι ορθογώνιο.
είναι ορθογώνιο. του τριγώνου
του τριγώνου  , κάθετες ευθείες επί των ευθειών πλευρών
, κάθετες ευθείες επί των ευθειών πλευρών  αντιστοίχως, του τριγώνου
αντιστοίχως, του τριγώνου  , συντρέχουν στο σημείο
, συντρέχουν στο σημείο  και επομένως τα τρίγωνα
και επομένως τα τρίγωνα  είναι Ορθολογικά.
είναι Ορθολογικά.
 Προκύπτει επομένως, ότι και οι δια των κορυφών
Προκύπτει επομένως, ότι και οι δια των κορυφών  του τριγώνου
του τριγώνου  , κάθετες ευθείες επί των ευθειών των πλευρών
, κάθετες ευθείες επί των ευθειών των πλευρών  αντιστοίχως, του τριγώνου
αντιστοίχως, του τριγώνου  , τέμνονται στο ίδιο σημείο το οποίο ταυτίζεται με το σημείο
, τέμνονται στο ίδιο σημείο το οποίο ταυτίζεται με το σημείο  , λόγω
, λόγω 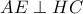 και
και  .
. κάθετη ευθεία επί την
κάθετη ευθεία επί την  , περνάει από το σημείο
, περνάει από το σημείο  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. .
.  φέρνω παράλληλη στη
φέρνω παράλληλη στη  που τέμνει την
που τέμνει την  στο
στο  . Τα τρίγωνα
. Τα τρίγωνα  όμοια γιατί
όμοια γιατί  .
. το ορθόκεντρο του
το ορθόκεντρο του 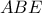 και
και  τα ύψη.
τα ύψη. το ορθόκεντρο του
το ορθόκεντρο του  και
και  τα ύψη.
τα ύψη. , ή ισοδύναμα
, ή ισοδύναμα  .
. .
. ή ισοδύναμα
ή ισοδύναμα  .
. .
.
 .
. , που προκύπτει από την ομοιότητα των
, που προκύπτει από την ομοιότητα των 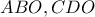 .
. ,
,  . Αυτό προκύπτει ΚΑΙ από λύση με Αναλυτική Γεωμετρία:
. Αυτό προκύπτει ΚΑΙ από λύση με Αναλυτική Γεωμετρία: ,
,  ,
,  ,
,  ΚΑΙ
ΚΑΙ  , έτσι ώστε η τομή
, έτσι ώστε η τομή  των διαγωνίων του τραπεζίου να ανήκει στον άξονα των
των διαγωνίων του τραπεζίου να ανήκει στον άξονα των  , προκύπτει ότι η τεταγμένη του
, προκύπτει ότι η τεταγμένη του  είναι η
είναι η  : η τεταγμένη αυτή καθ' εαυτή ΔΕΝ μας ενδιαφέρει, θα μας χρειαστεί όμως η προκύπτουσα ισότητα
: η τεταγμένη αυτή καθ' εαυτή ΔΕΝ μας ενδιαφέρει, θα μας χρειαστεί όμως η προκύπτουσα ισότητα  .
.  προκύπτει άμεσα ότι η τετμημένη του
προκύπτει άμεσα ότι η τετμημένη του  ισούται προς
ισούται προς  , οπότε από την
, οπότε από την  προκύπτει (μέσω συντελεστών διεύθυνσης) η
προκύπτει (μέσω συντελεστών διεύθυνσης) η  . Εύκολα προκύπτει τώρα ότι ο συντελεστής διεύθυνσης της
. Εύκολα προκύπτει τώρα ότι ο συντελεστής διεύθυνσης της  ισούται προς
ισούται προς  και, λόγω της
και, λόγω της  , προς
, προς  . Δεδομένου ότι ο συντελεστής διεύθυνσης της
. Δεδομένου ότι ο συντελεστής διεύθυνσης της  ισούται προς
ισούται προς  , η ζητούμενη καθετότητα
, η ζητούμενη καθετότητα  έχει αποδειχθεί.
έχει αποδειχθεί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες