



είναι σύνθετοι για κάθε τιμή του φυσικού

Συντονιστές: cretanman, silouan, rek2
 .
. ,θα έχουμε
,θα έχουμε  ,άρα
,άρα  .
. . Αρκεί να δούμε πόσο κάνει το
. Αρκεί να δούμε πόσο κάνει το  . Αν
. Αν  τότε από το θεώρημα Euler
τότε από το θεώρημα Euler  . Αν
. Αν  , τότε
, τότε  .
. .
. και εγώ
και εγώ  ; Τι θα διαλέξουμε για το Γ;
; Τι θα διαλέξουμε για το Γ; . Όμως
. Όμως  θα παρουμε λοιπόν mod 11. Θα γραψω λυση αργότερα.
θα παρουμε λοιπόν mod 11. Θα γραψω λυση αργότερα.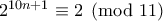
 και το ζητούμενο έπεται όπως και στους άλλους τρόπους.
και το ζητούμενο έπεται όπως και στους άλλους τρόπους.Μπορούμε και με επαγωγή δείχνοντας ότι ο καθένας διαιρείται με την μικρότερη τιμή του (τηνmatha έγραψε:Να αποδείξετε ότι οι αριθμοί
είναι σύνθετοι για κάθε τιμή του φυσικού
 ). Συγκεκριμένα από τους
). Συγκεκριμένα από τους  , αντίστοιχα.
, αντίστοιχα.

 βλέπουμε ότι το τελευταίο είναι πολλαπλάσιο του
βλέπουμε ότι το τελευταίο είναι πολλαπλάσιο του  . Με τη σειρά του βλέπουμε με πολλούς τρόπους ότι αυτό είναι πολλαπλάσιο του
. Με τη σειρά του βλέπουμε με πολλούς τρόπους ότι αυτό είναι πολλαπλάσιο του  . Π.χ. άμεσο από Fermat αφού
. Π.χ. άμεσο από Fermat αφού  και
και  . Το ίδιο αλλιώς:
. Το ίδιο αλλιώς:  .
.
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  . Αυτό είναι απλό αφού
. Αυτό είναι απλό αφού  και από Fermat
και από Fermat 

 . Με τη σειρά του αυτό είναι πολλαπλάσιο του
. Με τη σειρά του αυτό είναι πολλαπλάσιο του  καθώς
καθώς  και
και  .
. είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  , που έπεται από τις
, που έπεται από τις  και
και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες