 ώστε αν έχουμε
ώστε αν έχουμε  σημεία με ακέραιες συντεταγμένες στο επίπεδο τότε υπάρχουν δύο που το τετράγωνο της απόστασής τους είναι πολλαπλάσιο του
σημεία με ακέραιες συντεταγμένες στο επίπεδο τότε υπάρχουν δύο που το τετράγωνο της απόστασής τους είναι πολλαπλάσιο του  .
.Συντονιστές: cretanman, silouan, rek2
 ώστε αν έχουμε
ώστε αν έχουμε  σημεία με ακέραιες συντεταγμένες στο επίπεδο τότε υπάρχουν δύο που το τετράγωνο της απόστασής τους είναι πολλαπλάσιο του
σημεία με ακέραιες συντεταγμένες στο επίπεδο τότε υπάρχουν δύο που το τετράγωνο της απόστασής τους είναι πολλαπλάσιο του  .
.Ας μην ξεχαστεί όμως. Υπάρχει απλούστερη λύση;WLOG έγραψε:Πρόκειται για το πρόβλημα 2 της ολυμπιάδας της Βραζιλίας 2016.
https://artofproblemsolving.com/communi ... 90p7304182
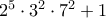 σημεία. Από την αρχή του περιστερώνα, μπορούμε να βρούμε δύο σημεία
σημεία. Από την αρχή του περιστερώνα, μπορούμε να βρούμε δύο σημεία  ώστε:
ώστε:

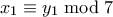



 και
και  . Επίσης:
. Επίσης:

 ορίζουμε το διάνυσμα
ορίζουμε το διάνυσμα 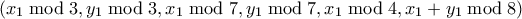
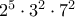 σημεία που να δίνουν διαφορετικά διανύσματα. Μένει να δείξουμε ότι το τετράγωνο της απόστασης δυο διαφορετικών διανυσμάτων δεν είναι πολλαπλάσιο του
σημεία που να δίνουν διαφορετικά διανύσματα. Μένει να δείξουμε ότι το τετράγωνο της απόστασης δυο διαφορετικών διανυσμάτων δεν είναι πολλαπλάσιο του  .
.  πρώτος με
πρώτος με  και
και  τότε
τότε  και
και  .
. και
και  και ότι είτε
και ότι είτε  είτε
είτε  . Θέλω να δείξω ότι
. Θέλω να δείξω ότι  .
. . Τότε
. Τότε  οπότε οι
οπότε οι  είναι άρτιοι. Έστω
είναι άρτιοι. Έστω  . Τότε
. Τότε  οπότε οι
οπότε οι 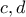 είναι επίσης άρτιοι, έστω
είναι επίσης άρτιοι, έστω  . Τότε
. Τότε  οπότε
οπότε  . Τότε
. Τότε  και
και  οπότε
οπότε  και
και  . Άτοπο αφού υποθέσαμε ότι αυτό δεν συμβαίνει.
. Άτοπο αφού υποθέσαμε ότι αυτό δεν συμβαίνει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες