 έτσι ώστε
έτσι ώστε  να είναι γινόμενο τεσσάρων( όχι απαραίτητα διαφορετικών ) πρώτων αριθμών
να είναι γινόμενο τεσσάρων( όχι απαραίτητα διαφορετικών ) πρώτων αριθμώνΣυντονιστές: cretanman, silouan, rek2
 έτσι ώστε
έτσι ώστε  να είναι γινόμενο τεσσάρων( όχι απαραίτητα διαφορετικών ) πρώτων αριθμών
να είναι γινόμενο τεσσάρων( όχι απαραίτητα διαφορετικών ) πρώτων αριθμώνΠαναγιώτη, θα με ενδιέφερε να δω μία απλή λύση, όπως ισχυρίζεσαι.Panagiotis11 έγραψε:Επαναφορά,δεν μου φαίνεται τόσο δύσκολο πρόβλημα
 .
.Ας γράψω μία λύση που από ότι φαίνεται είναι στο ίδιο μήκος κύματος με το μήνυμα του Παναγιώτη στο hide:Panagiotis11 έγραψε:Αν δεν έχει απαντηθεί με μία πιο κομψή λύση θα παραθέσω την απάντηση αύριο το απόγευμα.Μέχρι τότε θα αφήσω κάποια hide
2. Οι πρώτοι αριθμοί
 είναι περιττός. Επίσης δεν είναι πολλαπλάσιο του
είναι περιττός. Επίσης δεν είναι πολλαπλάσιο του  καθώς τα υπόλοιπα της διαίρεσής του για 3 είναι ένα από τα
καθώς τα υπόλοιπα της διαίρεσής του για 3 είναι ένα από τα  ή
ή  ή
ή  . Όμοια, εξετάζοντας τα
. Όμοια, εξετάζοντας τα  έως
έως  βλέπουμε ότι ο
βλέπουμε ότι ο  δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  . Εντελώς όμοια δεν είναι πολλαπλάσιο του
. Εντελώς όμοια δεν είναι πολλαπλάσιο του  . Άρα οι πρώτοι διαιρέτες του
. Άρα οι πρώτοι διαιρέτες του  είναι από
είναι από  και πάνω.
και πάνω.  , κατά σειρά μεγέθους: Είναι
, κατά σειρά μεγέθους: Είναι  και πάει λέγοντας. Ελέγχουμε τώρα ποιος είναι ο μικρότερος της μορφής
και πάει λέγοντας. Ελέγχουμε τώρα ποιος είναι ο μικρότερος της μορφής  . Ο
. Ο 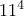 αποτυγχάνει (η διακρίνουσα είναι
αποτυγχάνει (η διακρίνουσα είναι  που δεν είναι τέλειο τετράγωνο). Ευτυχώς στον αμέσως επόμενο
που δεν είναι τέλειο τετράγωνο). Ευτυχώς στον αμέσως επόμενο  βρίσκουμε
βρίσκουμε  , που είναι η απάντηση στο πρόβλημά μας.
, που είναι η απάντηση στο πρόβλημά μας. προκύπτει στο δεύτερο βήμα της σάρωσης των
προκύπτει στο δεύτερο βήμα της σάρωσης των  Φαντάσου να ήταν π.χ. στο έβδομο, και μη χειρότερα. Θα κάναμε πράξεις σαν Λογιστές και όχι Μαθηματικοί.
Φαντάσου να ήταν π.χ. στο έβδομο, και μη χειρότερα. Θα κάναμε πράξεις σαν Λογιστές και όχι Μαθηματικοί. είναι γινόμενο δύο συνεχόμενων αριθμών άρα άρτιος αλλά
είναι γινόμενο δύο συνεχόμενων αριθμών άρα άρτιος αλλά  περιττός και
περιττός και 
 .Τώρα έυκολα παρατηρούμε ότι
.Τώρα έυκολα παρατηρούμε ότι 
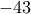 δεν είναι τέλειο τετράγωνο
δεν είναι τέλειο τετράγωνο  για
για 
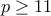
 ,όπου
,όπου 
 ,τότε
,τότε  .Πολλαπλασιάζοντας με 4 βρίσκουμε
.Πολλαπλασιάζοντας με 4 βρίσκουμε 
 ανάμεσα σε δύο συνεχόμενα τέλεια τετράγωνα.
ανάμεσα σε δύο συνεχόμενα τέλεια τετράγωνα.
 .Λόγω ανισότητας και επειδή
.Λόγω ανισότητας και επειδή  , εύκολα
, εύκολα 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες