Ένα παράδειγμα είναι ο
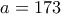
. Οι
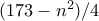
, όπου

θετικός ακέραιος, είναι θετικοί ακέραιοι για
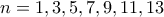
και είναι οι
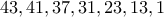
που είναι όλοι πρώτοι ή ίσοι με τη μονάδα.
Παρατηρούμε ότι
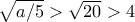
.
Αν

τότε για

παίρνουμε τους αριθμούς

και

. Τουλάχιστον ο ένας είναι άρτιος. Επίσης
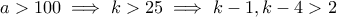
. Άρα δεν μπορεί να είναι και οι δύο πρώτοι και δεν έχουμε κάτι να αποδείξουμε.
Αν
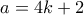
τότε
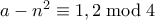
, οπότε κανένας από τους
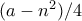
δεν είναι ακέραιος και δεν έχουμε κάτι να δείξουμε. Ομοίως και αν
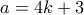
.
Ας υποθέσουμε λοιπόν ότι
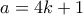
και ότι
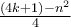
είναι πρώτος για κάθε ακέραιο
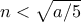
για τον οποίο ο
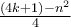
είναι θετικός ακέραιος. Ας υποθέσουμε επίσης προς άτοπο ότι υπάρχει
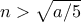
για τον οποίο ο
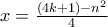
είναι θετικός ακέραιος αλλά σύνθετος. Μπορούμε να υποθέσουμε ότι ο

είναι ελάχιστος για τον οποίο ισχύει αυτή η ιδιότητα.
Έστω

ο μικρότερος πρώτος που διαιρεί τον

. Αφού

σύνθετος, τότε
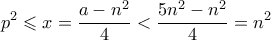
Ορίζουμε τώρα
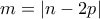
και παρατηρούμε ότι
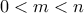
. Πράγματι αφού ο

είναι περιττός και ο
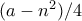
ακέραιος, τότε ο

είναι επίσης περιττός, άρα
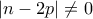
. Επίσης, αν
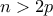
τότε

ενώ αν
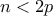
τότε
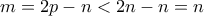
αφού ήδη δείξαμε ότι
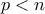
.
Ορίζουμε τώρα
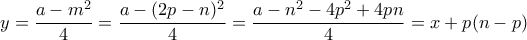
ο οπόιος είναι ακέραιος πολλαπλάσιος του

και άρα και αυτός σύνθετος. (Αφού επίσης
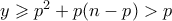
.
Άρα βρήκαμε
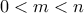
για τον οποίο ισχύει ότι ο
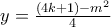
είναι θετικός ακέραιος αλλά σύνθετος. Από τον ορισμό του

πρέπει
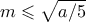
, αλλά αυτό είναι άτοπο αφού τότε ο

είναι πρώτος ή ίσος με

.
 , μεγαλύτερος του
, μεγαλύτερος του  . Στον πίνακα γράφτηκαν όλοι οι θετικοί ακέραιοι της μορφής
. Στον πίνακα γράφτηκαν όλοι οι θετικοί ακέραιοι της μορφής 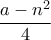 , όπου
, όπου  θετικός ακέραιος. Προέκυψε, ότι για
θετικός ακέραιος. Προέκυψε, ότι για 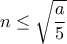 όλοι τους είναι πρώτοι. Να αποδείξετε, ότι και όλοι οι υπόλοιποι θετικοί ακέραιοι αριθμοί γραμμένοι στον πίνακα είναι πρώτοι ή ίση με την μονάδα.
όλοι τους είναι πρώτοι. Να αποδείξετε, ότι και όλοι οι υπόλοιποι θετικοί ακέραιοι αριθμοί γραμμένοι στον πίνακα είναι πρώτοι ή ίση με την μονάδα.  ;
;
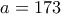 . Οι
. Οι 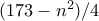 , όπου
, όπου 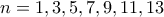 και είναι οι
και είναι οι 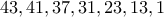 που είναι όλοι πρώτοι ή ίσοι με τη μονάδα.
που είναι όλοι πρώτοι ή ίσοι με τη μονάδα.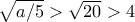 .
. τότε για
τότε για  παίρνουμε τους αριθμούς
παίρνουμε τους αριθμούς  και
και  . Τουλάχιστον ο ένας είναι άρτιος. Επίσης
. Τουλάχιστον ο ένας είναι άρτιος. Επίσης 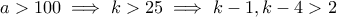 . Άρα δεν μπορεί να είναι και οι δύο πρώτοι και δεν έχουμε κάτι να αποδείξουμε.
. Άρα δεν μπορεί να είναι και οι δύο πρώτοι και δεν έχουμε κάτι να αποδείξουμε. 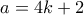 τότε
τότε 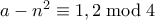 , οπότε κανένας από τους
, οπότε κανένας από τους 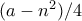 δεν είναι ακέραιος και δεν έχουμε κάτι να δείξουμε. Ομοίως και αν
δεν είναι ακέραιος και δεν έχουμε κάτι να δείξουμε. Ομοίως και αν 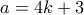 .
.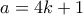 και ότι
και ότι 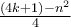 είναι πρώτος για κάθε ακέραιο
είναι πρώτος για κάθε ακέραιο 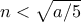 για τον οποίο ο
για τον οποίο ο 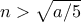 για τον οποίο ο
για τον οποίο ο 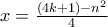 είναι θετικός ακέραιος αλλά σύνθετος. Μπορούμε να υποθέσουμε ότι ο
είναι θετικός ακέραιος αλλά σύνθετος. Μπορούμε να υποθέσουμε ότι ο  ο μικρότερος πρώτος που διαιρεί τον
ο μικρότερος πρώτος που διαιρεί τον  . Αφού
. Αφού 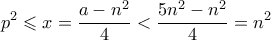
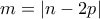 και παρατηρούμε ότι
και παρατηρούμε ότι 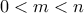 . Πράγματι αφού ο
. Πράγματι αφού ο 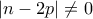 . Επίσης, αν
. Επίσης, αν 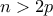 τότε
τότε  ενώ αν
ενώ αν 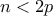 τότε
τότε 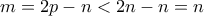 αφού ήδη δείξαμε ότι
αφού ήδη δείξαμε ότι 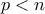 .
.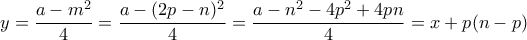
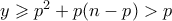 .
.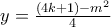 είναι θετικός ακέραιος αλλά σύνθετος. Από τον ορισμό του
είναι θετικός ακέραιος αλλά σύνθετος. Από τον ορισμό του 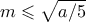 , αλλά αυτό είναι άτοπο αφού τότε ο
, αλλά αυτό είναι άτοπο αφού τότε ο  είναι πρώτος ή ίσος με
είναι πρώτος ή ίσος με  .
.