 όπου
όπου  . Το
. Το  συμβολίζει κορόνα και το
συμβολίζει κορόνα και το  γράμματα.
γράμματα.Μία ακολουθία
 λέγεται π-καλή εάν για κάθε
λέγεται π-καλή εάν για κάθε  ισχύει οτι η υπακολουθία
ισχύει οτι η υπακολουθία  περιέχει περισσότερες κορόνες απ'οτι γράμματα. Πχ για
περιέχει περισσότερες κορόνες απ'οτι γράμματα. Πχ για  έχουμε τις εξής π-καλές ακολουθίες:
έχουμε τις εξής π-καλές ακολουθίες:(1,1,1,1),(1,1,1,0),(1,1,0,1)
Παίζετε το εξής παίγνιο με έναν φίλο σας. Ο φίλος σας διαλέγει μια τυχαία ακολουθία με
 στοιχεία (απο τις
στοιχεία (απο τις  που υπάρχουν συνολικά). Εάν είναι π-καλή τότε κερδίζετε εσείς διαφορετικά κερδίζει ο φίλος σας. Επειδή ο φίλος σας θεωρεί οτι είναι εξαιρετικά απίθανο να βρεθεί μία ακολουθία οπου το πλήθος των κορόνων είναι σε κάθε χρονική στιγμή μεγαλύτερο απο αυτό των γραμμάτων, σας δίνει 1000 Ευρώ εάν κερδίσετε και εσείς του δίνετε μόνο 100 εάν χάσετε.
που υπάρχουν συνολικά). Εάν είναι π-καλή τότε κερδίζετε εσείς διαφορετικά κερδίζει ο φίλος σας. Επειδή ο φίλος σας θεωρεί οτι είναι εξαιρετικά απίθανο να βρεθεί μία ακολουθία οπου το πλήθος των κορόνων είναι σε κάθε χρονική στιγμή μεγαλύτερο απο αυτό των γραμμάτων, σας δίνει 1000 Ευρώ εάν κερδίσετε και εσείς του δίνετε μόνο 100 εάν χάσετε. Ωστόσο είστε κλεισμένος σε μία αίθουσα χωρίς βοήθεια υπολογιστή και ο φίλος σας θέλει απάντηση μέσα στην επόμενη ώρα. Δέχεστε να παίξετε το παίγνιο ή όχι?
(Συγγνώμη για την πολυλογία. Απλώς ήθελα να τονίσω οτι το πρόβλημα λύνεται χωρίς την χρήση υπολογιστή αν και χρειάζεται λίγες πράξεις (πάντως όχι
 ). Επιπλέον δεν είμαι σίγουρος αν η δυσκολία είναι για Αρχιμήδη οπότε το αφήνω στους συντονιστές να αποφασίσουν)
). Επιπλέον δεν είμαι σίγουρος αν η δυσκολία είναι για Αρχιμήδη οπότε το αφήνω στους συντονιστές να αποφασίσουν)
 για το πλήθος τον π-καλών ακολουθιών μήκους
για το πλήθος τον π-καλών ακολουθιών μήκους  .
.  . Πράγματι είναι απλό ότι αν η ακολουθία
. Πράγματι είναι απλό ότι αν η ακολουθία  είναι π-καλή το ίδιο ισχύει και για την ακολουθία
είναι π-καλή το ίδιο ισχύει και για την ακολουθία 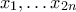 . Αντιστρόφως αν η
. Αντιστρόφως αν η  και
και  κορώνες.]
κορώνες.] όπου
όπου  είναι το πλήθος των π-καλών ακολουθιών
είναι το πλήθος των π-καλών ακολουθιών  οι οποίες έχουν
οι οποίες έχουν  όπου
όπου 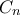 είναι οι αριθμοί Catalan. [Αναγκαστικά είναι
είναι οι αριθμοί Catalan. [Αναγκαστικά είναι  και η ακολουθία
και η ακολουθία  έχει
έχει  να έχει τουλάχιστον τόσους άσσους όσα μηδενικά. Αυτός όμως είναι ένας από τους γνωστούς ορισμούς της ακολουθίας Catalan.]
να έχει τουλάχιστον τόσους άσσους όσα μηδενικά. Αυτός όμως είναι ένας από τους γνωστούς ορισμούς της ακολουθίας Catalan.]
 . (Εύκολος υπολογισμός με βάση τον τύπο.) Έχουμε
. (Εύκολος υπολογισμός με βάση τον τύπο.) Έχουμε  . Άρα
. Άρα  και τέλος
και τέλος  .
. οπότε συμφέρει να παίξουμε.
οπότε συμφέρει να παίξουμε.
 αλλά δεν βλέπω κάποια άμεση συνδυαστική απόδειξη.
αλλά δεν βλέπω κάποια άμεση συνδυαστική απόδειξη. (με
(με  φυσικό,
φυσικό,  ακέραιο) το πλήθος των κ-καλών ακολουθιών μήκους
ακέραιο) το πλήθος των κ-καλών ακολουθιών μήκους 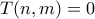 για
για  εφόσον οι άσσοι πρέπει να είναι πάντα περισσότεροι απο τα μηδενικά. Επιπλέον
εφόσον οι άσσοι πρέπει να είναι πάντα περισσότεροι απο τα μηδενικά. Επιπλέον 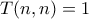
 εφόσον υπάρχει μονάχα μία ακολουθία με
εφόσον υπάρχει μονάχα μία ακολουθία με  προφανώς.
προφανώς.  . Τότε κάθε μία απο αυτές δημιουργείται είτε απο:
. Τότε κάθε μία απο αυτές δημιουργείται είτε απο: η οποία έχει
η οποία έχει  περισσότερους άσσους απο μηδενικά προσθέτοντας
περισσότερους άσσους απο μηδενικά προσθέτοντας  )
) περισσότερους άσσους απο μηδενικά προσθέτοντας
περισσότερους άσσους απο μηδενικά προσθέτοντας  .
. ισχύει
ισχύει 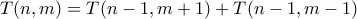

 . Αθροίζοντας την τελευταία γραμμή βρίσκουμε
. Αθροίζοντας την τελευταία γραμμή βρίσκουμε  άρα η πιθανότητα να κερδίσουμε είναι
άρα η πιθανότητα να κερδίσουμε είναι  και συνεπώς μας συμφέρει να παίξουμε.
και συνεπώς μας συμφέρει να παίξουμε.