Χρωματισμός κορυφών πολυγώνου

Διονύσιος Αδαμόπουλος · #1

Αντιγράφω το Πρόβλημα της Εβδομάδας OLY2017-B02 από την ΚΥ.Μ.Ε. η λύση του οποίου υπάρχει εδώ.

Με πόσους τρόπους μπορούμε να χρωματίσουμε ακριβώς k κορυφές ενός

-γώνου κόκκινες, έτσι ώστε να μην υπάρχουν δύο συνεχόμενες κορυφές που να είναι χρωματισμένες κόκκινες;

Η λύση που δίνω κάνει χρήση του λήμματος που είχα χρησιμοποιήσει και αποδείξει εδώ. Το γράφω κι εδώ με ισοδύναμο τρόπο θεωρώντας όμως ότι το

αναφέρεται στο συνολικό πλήθος των ψηφίων:

Λήμμα: Για να δημιουργήσουμε έναν

-ψήφιο δυαδικό αριθμό με

μη συνεχόμενους άσσους υπάρχουν $\displaystyle{\binom{n-k+1}{k}}$ τρόποι.

Ερχόμαστε τώρα στο αρχικό πρόβλημα.

Αντιστοιχούμε τις κορυφές του

-γώνου στα ψηφία ενός

-ψήφιου δυαδικού αριθμού. Οι άσσοι θα αντιστοιχούν στις κόκκινες κορυφές. Θα πρέπει να μην υπάρχουν 2 συνεχόμενοι άσσοι. Επιπλέον το πρώτο και το τελευταίο ψηφίο πρέπει να μην είναι και τα δύο άσσοι.

1η λύση

Για να βρούμε το πλήθος των χρωματισμών των κορυφών του πολυγώνου θα αφαιρέσουμε από το πλήθος των δυαδικών αριθμών του παραπάνω λήμματος το πλήθος των δυαδικών αριθμών που παραβιάζουν τις προϋποθέσεις του προβλήματος. Σε αυτούς το πρώτο και το τελευταίο ψηφίο τους θα είναι άσσος, ενώ το δεύτερο και το προτελευταίο ψηφίο τους θα είναι μηδενικό, δηλαδή ισοδύναμα είναι οι (n-4)

-ψήφιοι δυαδικοί αριθμοί με k-2

μη συνεχόμενους άσσους. Έχουμε λοιπόν:

$\displaystyle{\binom{n-k+1}{k} - \binom{n-4-k+2+1}{k-2} = \boxed {\binom{n-k+1}{k} - \binom{n-k-1}{k-2}}}$ τρόπους.

2η λύση

Βλέποντας τη σχετική λύση του κυρίου Δημήτρη στον αρχικό σύνδεσμο, προσάρμοσα την ιδέα που υπάρχει εκεί δίνοντας μια 2η λύση:

Έχουμε λοιπόν για το αριστερότερο ψηφίο του

-ψήφιου δυαδικού αριθμού δύο περιπτώσεις:

α) Να είναι

.

Άρα θα πρέπει να υπολογίσουμε πόσοι (n-1)

-ψήφιοι δυαδικοί αριθμοί υπάρχουν με

μη συνεχόμενους άσσους. Από το λήμμα προκύπτει:

$\displaystyle{\binom{n-1-k+1}{k} = \binom{n-k}{k}}$

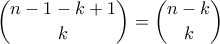
β) Να είναι

.

Άρα αναγκαστικά πρέπει το δεύτερο αλλά και το τελευταίο ψηφίο να είναι

. Άρα θα πρέπει να υπολογίσουμε πόσοι (n-3)

-ψήφιοι δυαδικοί αριθμοί υπάρχουν με k-1

μη συνεχόμενους άσσους. Από το λήμμα προκύπτει:

$\displaystyle{\binom{n-3-k+1+1}{k-1} = \binom{n-k-1}{k-1}}$

Επομένως έχουμε συνολικά: $\displaystyle{ \boxed{\binom{n-k}{k} + \binom{n-k-1}{k-1}}}$ τρόπους.

Το αποτέλεσμα της 2ης λύσης συμπίπτει με αυτό του κυρίου Δημήτρη. Όμως και αυτό της 1ης λύσης ουσιαστικά είναι ισοδύναμο.

Χρωματισμός κορυφών πολυγώνου

Χρωματισμός κορυφών πολυγώνου

Μέλη σε σύνδεση