 . Ορίζουμε συνάρτηση
. Ορίζουμε συνάρτηση  ως εξής:
ως εξής: και
και  για κάθε δύο θετικούς ακέραιους
για κάθε δύο θετικούς ακέραιους  με
με  .
. Να βρεθεί το πλήθος των ζευγών
 για τα οποία ο
για τα οποία ο  είναι περιττός.
είναι περιττός.Την έβαλα στον φάκελο της συνδυαστικής με tag άλγεβρα. Ένα από τα δύο ίσως να αλλάξει μετά την λύση.
Συντονιστές: Demetres, silouan
 . Ορίζουμε συνάρτηση
. Ορίζουμε συνάρτηση  ως εξής:
ως εξής: και
και  για κάθε δύο θετικούς ακέραιους
για κάθε δύο θετικούς ακέραιους  με
με  .
.  για τα οποία ο
για τα οποία ο  είναι περιττός.
είναι περιττός.
 .
. . Για κάθε ακέραιο
. Για κάθε ακέραιο 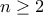 συμβολίζουμε με
συμβολίζουμε με 
 -οστής διαγωνίου (από πάνω αριστερά προς κάτω δεξιά) του πίνακα
-οστής διαγωνίου (από πάνω αριστερά προς κάτω δεξιά) του πίνακα  .
. με
με  ώστε ο αριθμός
ώστε ο αριθμός  να είναι περιττός είναι ίσο με
να είναι περιττός είναι ίσο με 

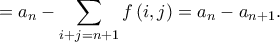
 με
με  ώστε ο αριθμός
ώστε ο αριθμός  να είναι περιττός είναι ίσο με
να είναι περιττός είναι ίσο με 
 για αρκετά μεγάλο
για αρκετά μεγάλο  (δηλαδή η αντίστοιχη
(δηλαδή η αντίστοιχη  -οστή διαγώνιος αποτελείται μόνο από μηδενικά).
-οστή διαγώνιος αποτελείται μόνο από μηδενικά). είναι μια φθίνουσα ακολουθία μη αρνητικών ακεραίων, οπότε είναι τελικά σταθερή, δηλαδή υπάρχουν μη αρνητικοί ακέραιοι
είναι μια φθίνουσα ακολουθία μη αρνητικών ακεραίων, οπότε είναι τελικά σταθερή, δηλαδή υπάρχουν μη αρνητικοί ακέραιοι  και
και  τέτοιοι, ώστε
τέτοιοι, ώστε  για κάθε
για κάθε  Αυτό σημαίνει ότι ο αριθμός
Αυτό σημαίνει ότι ο αριθμός  είναι άρτιος για κάθε ζεύγος
είναι άρτιος για κάθε ζεύγος  με
με  .
. και θεωρούμε τον ελάχιστο θετικό ακέραιο
και θεωρούμε τον ελάχιστο θετικό ακέραιο  για τον οποίο ισχύει
για τον οποίο ισχύει 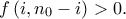
 ισχύει
ισχύει .
. έτσι, ώστε
έτσι, ώστε 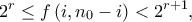 τότε έχουμε ότι
τότε έχουμε ότι  , πράγμα άτοπο. Ο ισχυρισμός έπεται.
, πράγμα άτοπο. Ο ισχυρισμός έπεται. ώστε ο αριθμός
ώστε ο αριθμός  να είναι περιττός είναι ίσο με
να είναι περιττός είναι ίσο με  .
. νομίσματα στο σημείο
νομίσματα στο σημείο  . Στο βήμα
. Στο βήμα  , για
, για  , κοιτάζουμε όλα τα σημεία της μορφής
, κοιτάζουμε όλα τα σημεία της μορφής  με
με  . Αν το σημείο έχει άρτιο αριθμό νομισμάτων, μεταφέρουμε τα μισά νομίσματα στο
. Αν το σημείο έχει άρτιο αριθμό νομισμάτων, μεταφέρουμε τα μισά νομίσματα στο  και τα μισά στο
και τα μισά στο  . Αν έχει περιττό αριθμό νομισμάτων, αφήνουμε ένα νόμισμα στο
. Αν έχει περιττό αριθμό νομισμάτων, αφήνουμε ένα νόμισμα στο  , και από τα υπόλοιπα, μεταφέρουμε τα μισά νομίσματα στο
, και από τα υπόλοιπα, μεταφέρουμε τα μισά νομίσματα στο  και τα μισά στο
και τα μισά στο  .
. βήματος, κάθε σημείο
βήματος, κάθε σημείο  με
με  έχει ακριβώς
έχει ακριβώς  νομίσματα. Επίσης, κάθε σημείο
νομίσματα. Επίσης, κάθε σημείο  με
με  , θα έχει είτε
, θα έχει είτε  είτε
είτε  νομίσματα ανάλογα με το αν ο
νομίσματα ανάλογα με το αν ο  είναι περιττός ή άρτιος.
είναι περιττός ή άρτιος. ώστε σε αυτό το βήμα στο
ώστε σε αυτό το βήμα στο  μεταφέρθηκε άρτιος αριθμός νομισμάτων. Το
μεταφέρθηκε άρτιος αριθμός νομισμάτων. Το  θα πάρει ακριβώς τα μισά από αυτά τα νομίσματα αφού εν υπάρχουν νομίσματα στο
θα πάρει ακριβώς τα μισά από αυτά τα νομίσματα αφού εν υπάρχουν νομίσματα στο 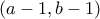 . Από την υπόθεση ο αριθμός αυτών των νομισμάτων θα είναι επίσης άρτιος. Το ίδιο και στο
. Από την υπόθεση ο αριθμός αυτών των νομισμάτων θα είναι επίσης άρτιος. Το ίδιο και στο  κ.ο.κ., άτοπο.
κ.ο.κ., άτοπο.  νομίσματα σε κάποιες θέσεις οι οποίες θα είναι ακριβώς οι θέσεις όπου τα
νομίσματα σε κάποιες θέσεις οι οποίες θα είναι ακριβώς οι θέσεις όπου τα  είναι περιττοί.
είναι περιττοί.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες