 τέτοιες ώστε
τέτοιες ώστε
για κάθε

Συντονιστές: achilleas, emouroukos, silouan
 τέτοιες ώστε
τέτοιες ώστε

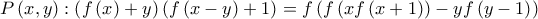
 έχουμε ότι:
έχουμε ότι:






 .
. τέτοιο, ώστε
τέτοιο, ώστε  .
. στη σχέση
στη σχέση  , βρίσκουμε ότι
, βρίσκουμε ότι

 και
και  .
. στη σχέση
στη σχέση  , βρίσκουμε ότι
, βρίσκουμε ότι
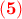 .
.

 ,
,
 .
.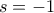 , τότε θα είχαμε ότι
, τότε θα είχαμε ότι  και από τη σχέση
και από τη σχέση 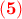 έχουμε ότι
έχουμε ότι  πράγμα άτοπο. Επομένως, από τη σχέση
πράγμα άτοπο. Επομένως, από τη σχέση  προκύπτει ότι
προκύπτει ότι  και από τη σχέση
και από τη σχέση 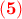 ότι
ότι 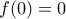 .
. και
και  τώρα γράφονται αντίστοιχα
τώρα γράφονται αντίστοιχα

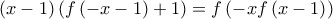

 .
. και
και  έχουμε ότι:
έχουμε ότι:

 .
. το
το  στη σχέση
στη σχέση  βρίσκουμε ότι:
βρίσκουμε ότι:
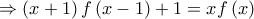

 .
. και
και  προκύπτει ότι:
προκύπτει ότι:


 .
. .
. τέτοιο, ώστε
τέτοιο, ώστε  Τότε, η σχέση
Τότε, η σχέση  δίνει ότι
δίνει ότι 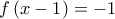 και άρα από τη σχέση
και άρα από τη σχέση  έχουμε ότι
έχουμε ότι 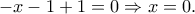
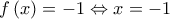 .
. (με
(με  ) τέτοιο, ώστε
) τέτοιο, ώστε  Τότε, από τη σχέση
Τότε, από τη σχέση  και τον Ισχυρισμό 3 προκύπτει ότι:
και τον Ισχυρισμό 3 προκύπτει ότι:
 δίνει τώρα ότι
δίνει τώρα ότι 

 με
με  .
. ισχύει και για
ισχύει και για  , δηλαδή ότι
, δηλαδή ότι 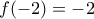 .
.  για
για  δίνει ότι
δίνει ότι  , ενώ η σχέση
, ενώ η σχέση  για
για  δίνει ότι
δίνει ότι 
 και
και  έπεται ότι για κάθε
έπεται ότι για κάθε  ,
,
 για κάθε
για κάθε  ,
,Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες